Типовые звенья в устройствах цифровой обработки сигналов. Цифровые фильтры, страница 5

На рис. 7.15 приведена структурная схема одного из возможных алгоритмов приближенного вычисления квадратного корня у = при изменении х от 0 до 1.

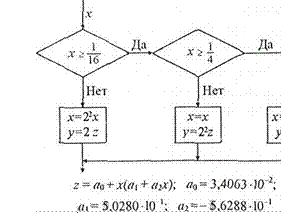
рис. 715

7.3.5 ЦИФРОВЫЕ АМПЛИТУДНЫЕ ОГРАНИЧИТЕЛИ

Назначение цифровых амплитудных ограничителей (АО) состоит в обеспечении стабильности амплитуды цифрового сигнала на их выходе при изменяющейся амплитуде цифрового сигнала на входе АО. На рис. 7.16 приведена укрупненная структурная схема  цифрового АО. В ее состав входят преобразователь Гильберта (ПГ) на входе, блок вычисления квадрата амплитуды „4 ², блок вы-

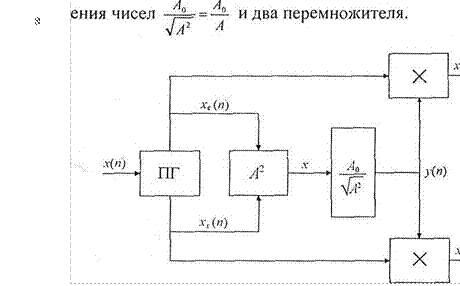
Рис. 7.16

Если на вход АО поступают выборки из сигнала х(п), то на выходах ПГ получим квадратурные компоненты из сигнала хс(п) = =А(п) cos по и „rs(n) sin по.

В блоке вычисления квадрата амплитуды выполняются операции по формуле хап) +  в результате чего получаем квадрат амплитуды входного сигнала. Далее числа А (п) поступают в блок вычисления чисел у(п) = АО / где Ао — заданная амплитуда на выходе АО. Как видим, в этом блоке необходимо выполнить операции извлечения квадратного корня и деления. Точное выполнение этих операций требует больших программных затрат. Для их уменьшения можно воспользоваться приближенВЫМ вычислением функции y=Ao/G по описанному в разделе 7.3.4 методу.

Для этого представляют функцию у =Ao/G полиномом (7.25) при заданном изменении аргумента х в пределах х, S х и фиксированном значении АО. Затем входное число х умножается на известное число 2±", чтобы выполнилось условие (7,26). После этого по (7.25) вычисляется значение у при аргументе 2²”х и получен-

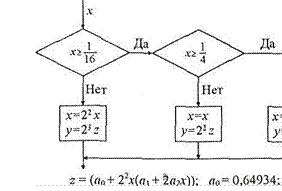
щ 0,77467; (12 ³ 0,76653

Рис. 7.17

ный результат умножается на число 2±пп . Описанная процедура вычислений поясняется формулой

                                                       (7.27)

На рис. 7.17 приведена структурная схема одного из возможных алгоритмов приближенного вычисления функции (7.27) при 1.

После умножения выборок хс(п) и xs(n) на числа уф) получаются выборки хсо(п) = = Ао cos по, .rso(n) =

= Ао sin по, принадлежащие квадратурным колебаниям со стабильНОЙ амплитудой АО.

Для повышения точности стабилизации амплитуды Ао сигнала можно увеличивать степень полинома в (7.25), сужать диапазон изменения аргумента х, + и использовать при этом больше условных переходов в процедуре вычисления функции (7.27).

Другой путь повышения точности АО — применение каскадного соединения нескольких амплитудных ограничителей.

7.3.6. ЦИФРОВЫЕ ГЕНЕРАТОРЫ

Цифровые генераторы формируют выборки через период тд = 1//⁷д из колебаний определенной формы — пилообразных, треугольных, трапецеидальных, прямоугольных, синусоидальных и т.д. Эти генераторы широко применяют в детекторах различных сигналов, в модуляторах, в системах фазовой автоподстройки частоты, в системах поиска и т.д. Кроме того, при квадратурной обработке сигналов необходимы генераторы, формирующие выборки из косинусной и синусной компонент гармонических колебаний. Такие генераторы называют обычно косинусно-синусными генераторами (КСГ). Важными характеристиками таких генераторов

Рис. 7.18

являются чистота спектра формируемых ими колебаний, погрешности квадратурных составляющих и линейность модуляционной характеристики.

Вначале рассмотрим наиболее простой в реализации на вычислителе цифровой генератор выборок из пилообразных колебаний. На базе этого генератора строят генераторы других форм колебаний.

Формирование выборок из пилообразных колебаний цифровым способом осуществляется по структурной схеме реализации алгоритма работы генератора пилообразных колебаний, изображенной на рис. 7.18.

Этот генератор работает по следующим разностным уравнениям:

z(n + 1) = z(n) + ап    при z(n) S М; z(n+ 1)  при z(n) (7.28)

где М — модуль суммирования; ап — коэффициент, задающий частоту пилообразных колебаний.

На рис. 7.19 приведены выборки z(n) из пилообразного колебания.