Типовые звенья в устройствах цифровой обработки сигналов. Цифровые фильтры, страница 2

Синтез нерекурсивных цифровых фильтров высокого порядка по заданным требованиям к АЧХ при линейной ФЧХ производится методом Фурье с применением оконных функций, методом наименьших квадратов и с использованием алгоритма Ремеза [14].

Рекурсивными называются фильтры с обратной связью (см. рис. 7.7), работа которых задается разностным уравнением

Здесь Вт — коэффициенты нерекурсивной части фильтра; Ап, — коэффициенты его рекурсивной части.

На рис. 7.7, б приведена так называемая каноническая схема рекурсивного фильтра. В этом фильтре меньше элементов задержки, чем в фильтре на рис. 7.7, а, а по свойствам они эквивалентны. Рекурсивные цифровые фильтры (РЦФ) также описываются системной функцией H(z), равной отношению Спреобразований Y(z) и X(z) от выходного у(п) и входного х(п) сигналов фильтра.

Для фильтров на рис. 7.7, а и 7.7, б системная функция Y(z) B0+Bp-t +B2f² +...+BM z не) =

Из разных методов расчета цифровых фильтров наибольшее распространение получил метод расчета РЦФ по аналоговому прототипу с применением билинейного преобразования. Вместе с тем в устройствах цифровой обработки сигналов довольно часто применяются двухконтурные и даже одноконтурные РЦФ. Такие фильтры могут быть рассчитаны по методу прямого синтеза. Проиллюстрируем это на примере.

Необходимо определить коэффициенты А, , А2 РЦФ второго порядка по известным резонансной частоте 00 и нижней границе полосы пропускания 01 при заданной неравномерности б в полосе пропускания.

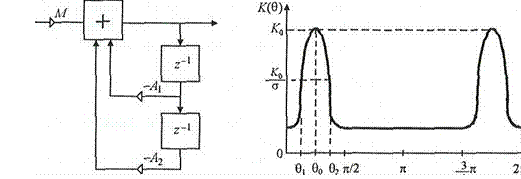
Структурная схема рекурсивного цифрового фильтра второго порядка (а) и его амплитудно-частотная характеристика (б) представлены на рис. 7.8. Системная функция РЦФ второго порядка (рис. 7.8, а)

                                                                                             2                                          2

где = Re^zl00 а = Reⁱ⁰⁰ — комплексно-сопряженные полюса системной функции РЦФ в полярных координатах; R — расстояние от начала координат до полюса в z — плоскости;  — нормированная к частоте дискретизации безразмерная частота резонанса. Из (7.19) следуют формулы, связывающие параметры R и 00 с коэффициентами РЦФ А, и „4:

а)

Рис. 7.8

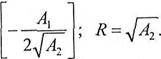      А, 00 ;      =R ² ; 00 =arccos(7.20)

Для перехода от H(z) к комплексному коэффициенту передачи К(ј0) необходимо в (7.19) сделать замену z= е/⁰, где 0 = 0)/FIl нормированная к безразмерная частота. В результате этой замены получим:

К(ј0) = [(1 —

Амплитудно-частотная характеристика РЦФ второго порядка есть модуль от К(ј0) и описывается выражением

       К(О) = {[l + R² —2R cos (О —             + R² —2R cos (О + 00)]}       .(7.21)

Построенная по этому выражению АЧХ для РЦФ второго порядка приведена на рис. 7.8, б. Зададимся неравномерностью б на нижней границе 01 полосы пропускания РЦФ и получим уравнение

                                                                                   (722)

где     [(1        + R² -2R cos 200)]-112 — коэффициент передачи РЦФ на резонансной частоте 00.

Возведем левую и правую части (7.22) в квадрат и с учетом (7.21) получим уравнение

                               0²(l            + R² - 21? cos 200) =

                     + R² - 2R cos (01 -                 + R² - 2R cos (01 - 00)].

После преобразований и замены переменной

²х(х + А) = (х +     + Cl),     (7.23) 0 где х — (1-R)2 • „4=1— cos 200', В,              cos (01 — 00); С]               cos (01 + 00).

Решим (7.23) относительно х. В результате

х = (р² +

                                                           2(о² —1)            6 ² —1

Тогда]? = 1 + х— [(1 +

Зная R и 00, по (7.20) определим коэффициенты А, и /12 РЦФ. Для обеспечения на частоте 00 единичного коэффициента передачи множитель М на входе РЦФ рассчитывается по формуле

7.32. ПРЕОБРАЗОВАТЕЛЬ ГИЛЬБЕРТА