Погрешности измерений. Измерение токов и напряжений. Приборы анализа электрических сигналов. Измерение напряженности поля и помех, страница 5

невозможно, но пользуясь (1.3) легко получить

1) ;

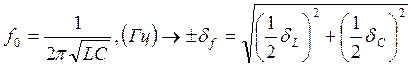2) ;

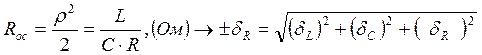3) .

А зная  легко найдем абсолютную случайную погрешность ,так как  .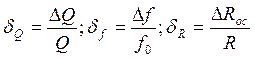

            Результат измерения всегда есть измеренная величина ± абсолютная ошибка:  и т.д.

            Законы распределения погрешностей

            Ранее мы рассматривали нормальные распределения погрешностей (рисунок 1.1), которое имеет место при большом числе испытаний в равнозначных условиях. Но в технике связи бывают случаи испытаний в количестве не более 10, что недостаточно с математической точки зрения. Поэтому закон распределения будет отличатся от нормального (Гауссового) – это закон распределения Стьюдента. Цифровые приборы, которые вытесняют  в настоящее время аналоговые, обычно имеют равномерный закон распределения (рисунок 1.4).

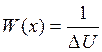
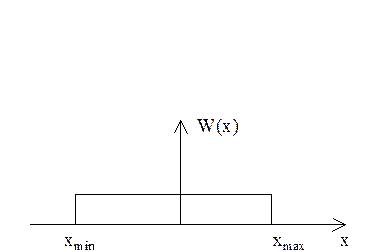, где - шаг квантования по уровню. Цифровые приборы считают целое число уровней (через интервал по напряжению -  В).

            Для оценки погрешностей для любого закона распределения надо найти

                      Рисунок 1.4

дисперсию случайного процесса – Д[x] (мощность разброса ошибок) или ее среднеквадратическое значение  - напряжение в вольтах.

            При цифровых измерениях 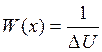, а , где m₁ и m₂ – первый и второй моменты ССП. Если мы будем искать σ вблизи 0, то есть m₁=0, то 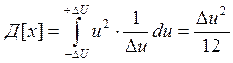, а 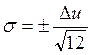 [В] – это СКО цифровых приборов.

            Для нормального закона, который хорошо описан и его значения табулированы (имеются готовые таблицы интеграла вероятности) максимальная погрешность при Р_д=0.9, Δ _д=2σ и при Р_д=0.95, Δ _д=3σ. На практике говорят, что при нормальном законе распределения максимальная ошибка не выходит за 3σ.

            В свою очередь , где Δ_i – погрешности отдельных n измерений.

            При малом числе измерений (n) необходимо вносить поправку в максимальную погрешность на коэффициент Стьюдента – t_n, который также табулирован и зависит от n и Р_д.

            Правила обработки ряда экспериментальных измерений

            На практике n10, поэтому для математически правильной оценки результатов поступают следующим образом:

1.  Если измеряется некоторая ФВ «А», то в результате имеем n отсчетов. Наиболее достоверное (среднее значение ФВ)

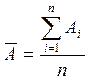                                                                                              (1.4)

2. Находятся первые разности наблюдения

                                                                               (1.5)

При этом оценивается близость распределения к нормальному закону: 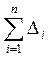 должна стремится к нулю (ошибки «вверх» и «вниз» равновероятны).

3.  Находится СКО ряда наблюдений:

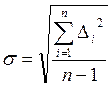                                                                                (1.6)

Это среднеквадратичная ошибка однократного измерения. Если говорить об СКО найденного среднего значения, то 

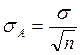                                                                                     (1.7)

Формула (1.7) показывает, что в результате множества измерений СКО уменьшается   раз! Чтобы прибором класса 10.0 получить ответ с погрешностью 1.0, необходимо провести 100! измерений.

4. Зная конечное число измерений – n и доверительную вероятность Р_д по       таблице находим коэффициент Стьюдента t_n и окончательно имеем    доверительный интервал измерений

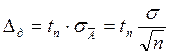                     (1.8)

На основании чего можно записать:

                           (1.9)

Например, измеряли напряжение с Р_д=0.9. Тогда получили  и . Ответ: .

2 ИЗМЕРЕНИЕ ТОКОВ И НАПРЯЖЕНИЙ

Эти физические величины взаимосвязаны между собой через постоянный коэффициент – сопротивление: 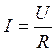, поэтому на низких частотах (0 – 20 кГц) они чаще всего измеряются однотипными электромеханическими приборами (ЭМП), в которых, как говорит само название, происходит преобразование электрической энергии в механические перемещения указателей (стрелок).

Сами по себе ЭМП подразделяются на:

1.  Магнитоэлектрические приборы (МЭ).

2.  Электромагнитные (ЭМ).

3.  Электродинамические (ЭД).