Погрешности измерений. Измерение токов и напряжений. Приборы анализа электрических сигналов. Измерение напряженности поля и помех, страница 4

3.  Методологические (заложены в не совсем верное математическое описание прибора). Например, 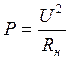, измеряем U² , считая R_н=const (75 Ом), но R_н зависит от U! (оно греется при больших U и меняет значение, и мы будем систематически «недовешивать» с ростом U)

4.  Погрешности вследствие механических (или электрических) люфтов.

Необходимо подчеркнуть, что по ГОСТу запрещается работать с приборами, имеющими систематическую погрешность. Величина Δс и ее знак может быть определена методом сравнения (поверкой) с образцовым прибором  (класс точности на один порядок выше поверяемого) или образцовыми мерами (набором гирь для весов). Оставшаяся неисключенная систематическая погрешность (НСП) не должна превышать 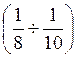от случайной (скрываться в случайной).

Случайные погрешности не могут быть исключены по своей природе. Единственный метод их уменьшение – увеличение числа измерений. Недаром портной семь раз отмеряет, прежде чем отрезать! Но при этом точность измерения увеличивается в  раз! Например, прибором класса 10.0 получим в 10 раз лучшую точность при 100 измерениях с последующим усреднением результатов:

                       

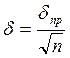
Поэтому все последующее внимание уделим вопросам правила учета случайных погрешностей.

Суммирование погрешностей в многоблоковых устройствах при прямых измерениях

В технике связи, как отмечалось выше, широко используются измерительные приборы. Например, электронные вольтметры высоких частот содержат (рисунок 1.2): диод – Д, превращающий амплитуду U_х высокочастотных колебаний в U₀, УПТ – усилитель постоянного тока для расширения чувствительности прибора и измерительный механизм – ИМ (вольтметр постоянного тока).

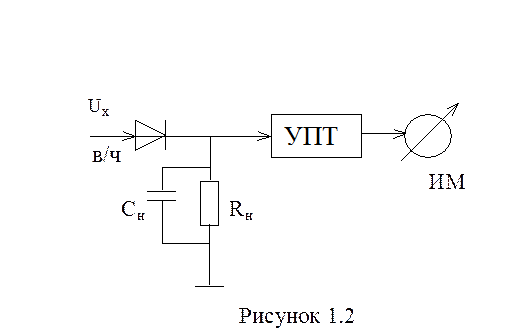Таким образом вольтметр в/ч состоит из трех независимых элементов (детектор, УПТ и ИМ), каждый из которых может обладать свойственными только ему определенными погрешностями.

Естественно, что систематическая суммарная погрешность будет найдена простым арифметическим суммированием

                                                 ,

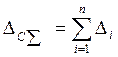в нашем случае .

            Но каждый из элементов обладает и своей собственной случайной погрешностью. Суммарная дисперсия независимых событий равно сумме дисперсий, то есть

                                                         (1.1)

или для относительных случайных величин

                                                ,

то есть определяется как среднеквадратическая величина.

            Например, диод обладает разбросом ±1%,  УПТ ±2%, а δ_ср=1%, то результирующая погрешность всего электронного вольтметра будет

                                               .

            Суммирование погрешностей при косвенных измерениях

            Если мы измеряем ФВ «А», которая, в свою очередь, зависит от параметров x, y, z А=f(x,y,z), то есть мы измеряем величины x, y, z с какими-то погрешностями, но хотим получить ΔА=?. Тогда

                                                             (1.2)

            Уравнение (1.2) носит название полное уравнение погрешностей, в котором частные производные – это коэффициенты влияния параметров (x, y, z) на результат. Для практических целей (1.2) может быть упрощено при нахождение относительной погрешности 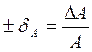. Тогда если , то

                                                                          (1.3)

            Относительная случайная погрешность косвенных измерений есть среднеквадратическое значение погрешностей отдельных параметров, умноженных на степень, в которой они находятся в формуле.

            Например: Очень часто инженер рассчитывает колебательные контура вида рис. 1.3. При этом есть возможность замерить L, C и R, но с какими-то погрешностями  (или купили готовые элементы, на которых стоит разброс их величин).

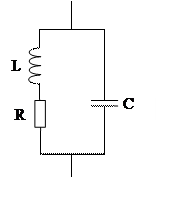            В колебательном контуре может интересовать резонансная частота, эквивалентное сопротивление – R_oс, добротность контура и т.д. Дать формулу для расчета ошибок косвенных измерений на все случаи жизни

            Рисунок 1.3