Погрешности измерений. Измерение токов и напряжений. Приборы анализа электрических сигналов. Измерение напряженности поля и помех, страница 3

1 ПОГРЕШНОСТИ ИЗМЕРЕНИЙ И ИХ КЛАССИФИКАЦИЯ

Погрешности измерений – это отклонение результатов измерений от истинного значения в результате влияния множества посторонних факторов: изменения окружающей температуры, напряжения источника питания, трение в скользящих парах, нестабильности контактов и т.п.

Ошибки измерений – это неправильные результаты измерений из-за неквалифицированных действий.

Вследствие наличия множества влияющих факторов, погрешности – это вероятностные процессы, которые могут быть оценены только в результате статической обработки (учет большого числа измерений n > 100).

Допустим, что мы решили измерить напряжение в лабораторной сети, которое должно быть 220 В. В результате большого числа измерений мы получили функцию (гистограмму) плотности вероятности от напряжения (рисунок 1.1)

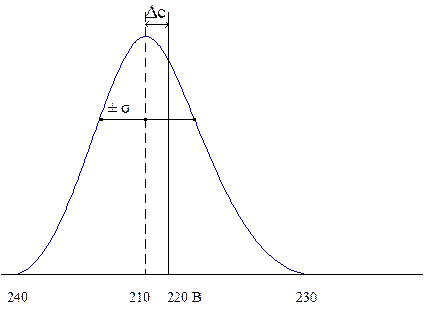
Рисунок 1.1

Результат множества измерений дал наиболее вероятное (чаще всего встречающееся) значение напряжения – 210 В 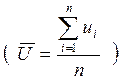, которое при конечном числе измерений есть среднеарифметическое ( ) значение.

При этом мы обнаружили систематическое отклонение в сторону занижения от истинного  В, которое носит название абсолютной систематической погрешности результатов измерения. Это отклонение Δс имеет вполне определенный знак и может быть определено и как относительное отклонение 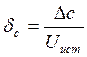 - безразмерная величина (или %).

  Но с точки зрения правил обработки случайных процессов мы вводим среднеквадратическое отклонение от среднего значения ±σ (В), которое равно , где  - дисперсия процесса. Дисперсия – это мощность рассеяния результатов вокруг среднего значения. Если сеть очень хорошая , то эта σ будет уменьшаться, группируясь вокруг , при этом мы не можем гарантировать его знак и такая погрешность называется случайной и ей присваивается знак ±. Случайная погрешность так же может быть и относительной .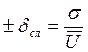

Подобное распределение погрешностей называется гауссовым (или нормальным), когда отдельные отклонения симметричны относительно среднего значения и быстро убывают с ростом их величины (большие погрешности маловероятны).

Однако величина дисперсии соответствует площади (вероятности события) равной 0,5, то есть внутри ±σ лежит 50% всех измерений и 50% - вне ее. На практике это называется срединной ошибкой, то есть если мы зададимся возможными разносами контролируемого параметра, то только 50% будут удовлетворять ему. Поэтому в инженерной практике задаются уровнем доверительной вероятности случайных отклонений Р_д=(1 - Р_ош), то есть оставляем неучтенной площадь кривой Р_ош. Например, если мы хотим измерить ФВ с точностью ±10%, Р_ош=0.1, то доверительная вероятность будет 0.9.

Величина случайной погрешности, соответствующая уровню Р_д носит название доверительного интервала.

Результат множества измерений при этом следует записать:

                                                 В

Например, U_0,9=(210±10) В. Это обозначает, что наиболее вероятное напряжение в сети равно 210 В и в 90% случаях оно занимает интервал ±10 В. Обычно Р_д задается из технических требований, либо сам инженер для грубых измерений принимает Р_д=0.9 (Р_ош=10%), либо для точных - Р_д=0.99 (Р_ош=1%). Но это далеко не всегда; бывают весьма точные измерения, когда Р_д  1. Указанные погрешности измерений могут быть вызваны как внешними причинами, так и конструктивными свойствами самого измерительного механизма. При этом величина максимальной погрешности, отнесенная к конечному значению шкалы прибора носит название приборной погрешности - 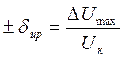, а если она выражена в % - класс точности прибора. Вольтметр класса 0.1 имеет случайную погрешность ±1%, а класса 10.0 - ±10%.

Систематические погрешности, имеющие определенный знак (или +, или – ) принято делить по причинам их возникновения на

1.  Инструментальные (плохая линейка для измерения длины)

2.  Ошибки оператора (индивидуальные особенности человека, параллакс)