37
Если на вход дискретной цепи с импульсной характеристикой h(n) поступает последовательность x(n), то сигнал на выходе y(n) равен
1)
y(n)=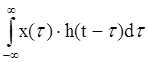 ;
;
2)
y(n)= ;
;
3)
y(n)=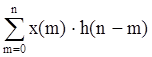 ;
;
4)
y(n)=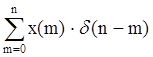 .
.
38
Теореме дискретной свертки соответствует выражение
1) y(n)=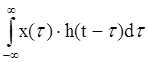 ;
;
2)
y(n)= ;
;
3)
y(n)=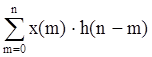 ;
;
4)
y(n)=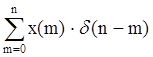 .
.
39
Если число отсчетов входного сигнала равно N, а число отсчетов импульсной характеристики дискретной цепи равно M, то число отсчетов выходного сигнала равно
1) N;
2) M;
3) N+M;
4) N+M–1.
40
На вход цепи поступает последовательность отсчетов x(n)={1;1}. Импульсная характеристика цепи h(n)={0;1}. Выходная последовательность y(n) равна
1) {1;1;0};
2) {0;1;0};
3) {0;1;1};
4) {1;1;1}.
41
Если импульсная характеристика аналоговой цепи h(t)=e–0,5t, то значение отсчетов импульсной характеристики соответствующей ей дискретной цепи, имеющей интервал дискретизации Т=2сек., будут равны
1) {1;0;0;…};
2) {0;1;1;…};
3) {1;e–1;e–2;e–3;…};
4) {1;e1;e2;e3;…}.
42
Если импульсная характеристика линейной дискретной цепи h(n) задана тремя отсчетами, а входная последовательность x(n) – четырьмя, то число отсчетов y(n) на входе цепи равно
1) 3;
2) 4;
3) 5;
4) 6.
43
Количество отсчетов выходной последовательности дискретной ЛЭЦ, имеющей импульсную характеристику h(n)={h0;h1;h2;h4} при входной последовательности x(n)={x0;x1;x2} равно
1) 3;
2) 4;
3) 5;
4) 6.
44
Выходная последовательность y(n) линейной дискретной цепи, имеющей импульсную характеристику h(n)={1;0} при поступлении на вход отсчетов x(n)={–1;1} равна
1) {0;1;1};
2) {1;0;–1};
3) {–1;1;0};
4) {1;–1;0}.
45
Выходная последовательность y(n) линейной дискретной цепи, имеющей импульсную характеристику h(n)={0;1} при поступлении на вход отсчетов x(n)={1;–1} равна
1) {0;1;1};
2) {1;–1;0};
3) {–1;1;0};
4) {0;1;–1}.
46
Импульсной характеристикой дискретной цепи
называется реакция цепи на
1) единичную дискретную функцию 1(n);
2) ?дискретную δ-функцию δ(n);
3) дискретную функцию е–αn.
47
Спектральная плотность непериодического аналогового сигнала находится как
1) преобразование Лапласа;
2) Z-преобразование;
3) ?прямое преобразование Фурье;
4) обратное преобразование Фурье.
48
Спектральная плотность непериодического аналогового сигнала x(t) находится по формуле
1) X(jω)=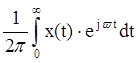 ;
;
2) X(jω)=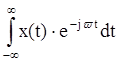 ;
;
3) X(jω)=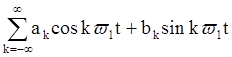 ;
;
4) X(jω)=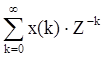 .
.
49
Комплексные амплитуды периодического аналогового сигнала x(t) находится по формуле
1) X(jω)=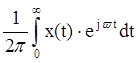 ;
;
2) X(jnω)=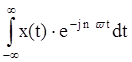 ;
;
3) X(jω)=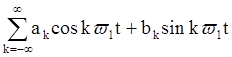 ;
;
4) X(jω)=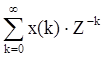 .
.
50
Спектральная плотность непериодического дискретного сигнала является
1) непрерывной функцией частоты;
2) дискретной функцией частоты;
3) непрерывной периодической функцией частоты;
4) дискретной периодической функцией частоты.
51
Комплексный спектр периодического дискретного сигнала является
1) непрерывной функцией частоты;
2) дискретной функцией частоты;
3) непрерывной периодической функцией частоты;
4) дискретной периодической функцией частоты.
52
Спектральная плотность непериодического дискретного сигнала (частота дискретизации равна ωд ) определяется выражением
1) X(ejωt)=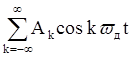 ;
;
2) X(ejωt)=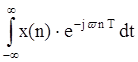 ;
;
3) X(ejωt)=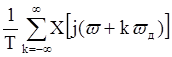 ;
;
4) X(ejωt)=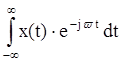 .
.
53
Если частота дискретизации сигнала ωд<2ωв, гле ωв – верхняя частота спектра дискретизируемого сигнала x(t), то модуль спектра |X(ejωT)| дискретного сигнала имеет вид
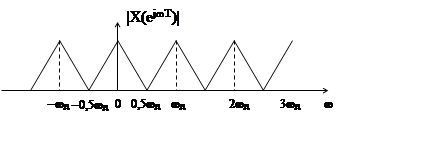 |
1)
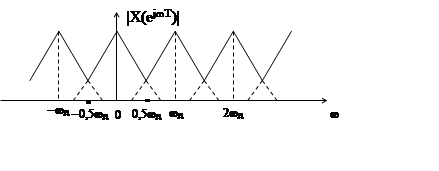 |
2)
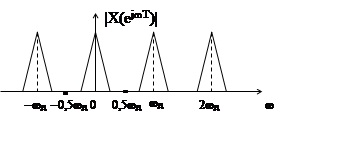 3)
3)
54
Если частота дискретизации сигнала ωд=2ωв, гле ωв – верхняя частота спектра дискретизируемого сигнала x(t), то модуль спектра |X(ejωT)| дискретного сигнала имеет вид
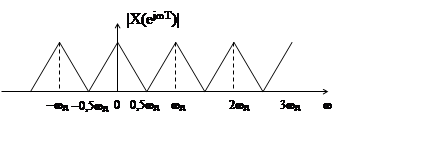 |
1)
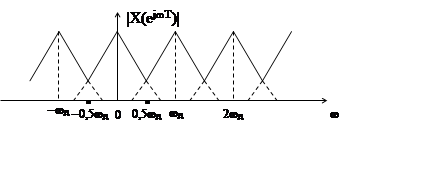 |
2)
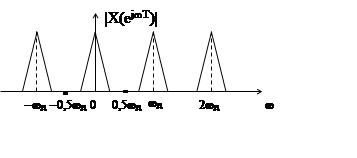 |
3)
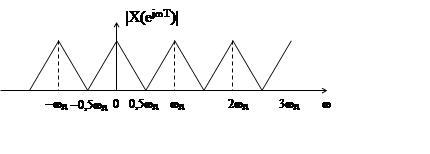 |
55
Если частота дискретизации сигнала ωд>2ωв, гле ωв – верхняя частота спектра дискретизируемого сигнала x(t), то модуль спектра |X(ejωT)| дискретного сигнала имеет вид
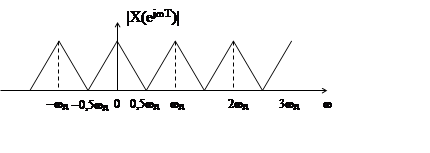 1)
1)
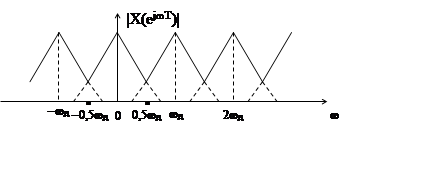 |
2)
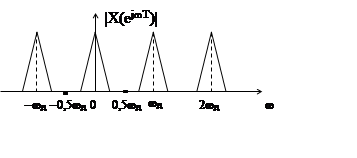 3)
3)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.