Теорема дискретной свертки. Число отсчетов импульсной характеристики дискретной цепи. Импульсная характеристика аналоговой цепи, страница 4

92

Линейной дискретной цепи, имеющей структурную схему

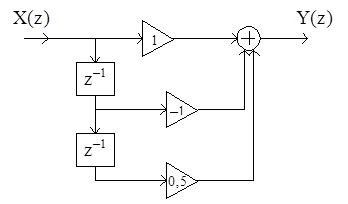
соответствует передаточная функция H(z)

1)  1+z^–1–0,5z^–2;

2)  1·z^–1–z^–2+0,5·z^–3;

3)  –1+z^–1–0,5z^–2;

4)  1–z^–1+0,5·z^–2.

93

Линейной дискретной цепи, имеющей структурную схему                    

соответствует сигнал на выходе Y(z), равный

1)  X(z)+z^–1X(z)–0,5z^–2X(z);

2)  X(z)–z^–1X(z)+0,5z^–2X(z);

3)  – X(z)+z^–1X(z)–0,5z^–2X(z);

4)  z^–1X(z)–z^–2X(z)+0,5z^–3X(z).

94

Дискретной линейной цепи, имеющей структурную схему

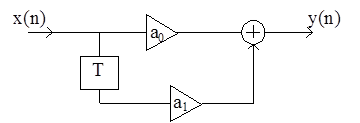
соответствует импульсная характеристика h(n)

1)  {0;a₀;a₁};

2)  {a₀;a₁};

3)  {–a₀;–a₁};

4)  {a₀;–a₁}.

95

Дискретной линейной цепи, имеющей структурную схему

соответствует сигнал на выходе y(n)

1)  1+a₀x_(n)+a₁x_(n–1);

2)  a₀x_(n)–a₁x_(n–1);

3)  a₀x_(n–1)+a₁x_(n);

4)  a₀x_(n)+a₁x_(n–1).

96

Дискретной линейной цепи, имеющей структурную схему

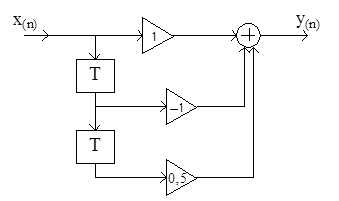
соответствует импульсная характеристика h(n)

1)  {1;1;0,5};

2)  {1;–1;–0,5};

3)  {–1;1;–0,5};

4)  {1;–1;0,5}.

97

Дискретной линейной цепи, имеющей структурную схему

соответствует сигнал на выходе y(n)

1)  x_(n)+x_(n–1)–0,5x_(n–2);

2)  x_(n)–x_(n–1)+0,5x_(n–2);

3)  – x_(n)+x_(n–1)–0,5x_(n–2);

4)  x_(n)+x_(n–1)+0,5x_(n–2).

98

Частотной характеристикой линейной дискретной цепи называется отношение

1)  ;

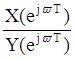2)  ;

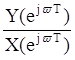3)  ;

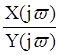4)  .

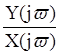99

Переход к частотной характеристике H(e^jωT) дискретной линейной цепи осуществляется заменой в системной функции H(z)

1)  z^–1=e^jωT;

2)  z=e^–jωT;

3)  z=e^jωT;

4)  z^–n=e^jωT.

100

Модуль |H(e^jωT)| частотной характеристики линейной дискретной цепи является

1)  непериодической функцией частоты;

2)  ?четной периодической функцией частоты;

3)  нечетной периодической функцией частоты.

101

Аргумент φ(e^jωT) частотной характеристики линейной дискретной цепи является

1)  непериодической функцией частоты;

2)  четной периодической функцией частоты;

3)  ?нечетной периодической функцией частоты.

102

Период повторения частотной характеристики линейной дискретной цепи равен

1)  верхней частоте спектра исходного аналогового сигнала f_в;

2)  частоте дискретизации f_д;

3)  удвоенной частоте дискретизации 2f_д;

4)  половине частоте дискретизации 0,5f_д.

103

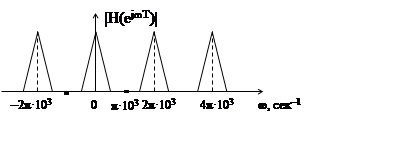Частотной характеристике линейной дискретной цепи

соответствует частота дискретизации f_д (Гц)

1)  2π·10³ сек^–1;

2)  1·10³ Гц;

3)  π·10³ сек^–1;

4)  0,5·10³ Гц.

104

Если частота дискретизации f_д равна 10кГц, то период повторения частотной характеристики линейной дискретной цепи равен

1)  5кГц;

2)  10кГц;

3)  20кГц;

4)  π·10 сек^–1.

105

Частотная характеристика H(e^jωT) линейной дискретной цепи является

1)  непрерывной непериодической функцией частоты;

2)  непрерывной периодической функцией частоты;

3)  дискретной непериодической функцией

частоты;

4)  дискретной периодической функцией частоты.

106

Передаточной функции линейной дискретной цепи H(z)=1+z^–1+0,5z^–2 соответствует частотная характеристика H(e^jωT)

1)  1+e^–jωT–0,5 e^–2jωT;

2)  1–e^–jωT+0,5 e^–2jωT;

3)  1+e^–jωT+0,5 e^–2jωT;

4)  1–e^–jωT–0,5 e^–2jωT.

107

Частотная характеристика линейной дискретной цепи рассматривается на интервале

1)  0÷f_д;

2)  0÷2f_д;

3)  0÷0,5f_д;

4)  –f_д÷f_д.