Теорема дискретной свертки. Число отсчетов импульсной характеристики дискретной цепи. Импульсная характеристика аналоговой цепи, страница 3

1)  e^–α·nT·z^–n;

2)  (e^–α·T·z^–1)ⁿ;

3)  1+e^–α·T·z^–1+e^–2α·T·z^–2+…;

4)  1–e^–α·T·z^–1–e^–2α·T·z^–2–…

75

Z–преобразование  X(z)  дискретного  сигнала x(n)=aⁿ, n≥0 для значения а=0,8 равно

1)  1+0,8·z^–1+0,64·z^–2+0,512·z^–3+…

2)  1+0,8·z^–1–0,64·z^–2+0,512·z^–3–…

3)  1+z^–1+z^–2+z^–3+…

4)  1–0,8·z^–1+0,64·z^–2–0,512·z^–3+…

76

Z–преобразование  X(z)  дискретного  сигнала x(n)=aⁿ, n≥0 для значения а= = –0,8 равно

1)  1+0,8·z^–1+0,64·z^–2+0,512·z^–3+…

2)  1+0,8·z^–1–0,64·z^–2+0,512·z^–3–…

3)  1+z^–1+z^–2+z^–3+…

4)  1–0,8·z^–1+0,64·z^–2–0,512·z^–3+…

77

Если Z–преобразование дискретного сигнала X(z)=0,5–1·z^–1+1·z^–2–0.5·z^–3, то отсчеты сигнала x(n) равны

1)  {–1;1;0;1};

2)  {–0,5;1;–1;0,5};

3)  {0,5;–1;1;–0,5};

4)  {1;–1;1;–1}.

78

Отношение Z–изображений выходного и входного дискретных сигналов дискретной цепи называется

1)  передаточной функцией;

2)  частотной характеристикой;

3)  фазовой характеристикой;

4)  импульсной характеристикой.

79

Передаточной (системной) функцией H(z) дискретной цепи называется отношение

1)  ;

2)  ;

3)  ;

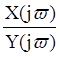4)  .

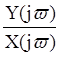80

Передаточная функция H(z) элемента задержки на 1 интервал дискретизации T равна

1)  Z¹;

2)  Z^–1;

3)  Z²;

4)  Z^–2.

81

Передаточная функция H(z) дискретной цепи

 Равна

1)  Z;

2)  Z^–1;

3)  Z²;

4)  Z^–2.     

82

Сигнал на Y(z) выходе дискретной цепи

Равен

1)  X(z)·Z;

2)  X(z)·Z^–1;

3)  X(z)·Z²;

4)  X(z)·Z^–2.

83

Сигнал Y(z) на выходе дискретной цепи

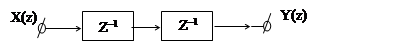                                                                                                        Равен

1)  X(z)·Z;

2)  X(z)·Z^–1;

3)  X(z)·Z²;

4)  X(z)·Z^–2.

84

Системная функция H(z) линейной дискретной цепи, имеющей импульсную характеристику h(n)={1;–1;1}, равна

1)  1+z^–2;

2)  –1+z^–1–z^–2;

3)  z^–1+z^–2;

4)  1– z^–1+z^–2.

85

Системная функция H(z) линейной дискретной цепи, имеющей импульсную характеристику h(n)={0;1;–1}, равна

1)  1+z^–2;

2)  –1+z^–1–z^–2;

3)  z^–1–z^–2;

4)  1– z^–1+z^–2.

86

Системная функция H(z) линейной дискретной цепи, имеющей импульсную характеристику h(n)={–1;1;–1}, равна

1)  1+z^–2;

2)  –1+z^–1–z^–2;

3)  z^–1+z^–2;

4)  1– z^–1+z^–2.

87

Системная функция H(z) линейной дискретной цепи, имеющей импульсную характеристику h(n)={1;0;–1}, равна

1)  1–z^–2;

2)  –1+z^–1–z^–2;

3)  z^–1+z^–2;

4)  1– z^–1+z^–2.

88

Линейной дискретной цепи, имеющей структурную схему

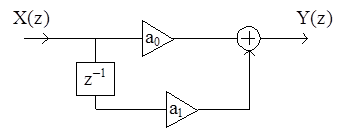
соответствует передаточная функция H(z)

1)  a₀z⁰–a₁z^–1;

2)  a₀z^–1+a₁z¹;

3)  a₀+a₁z^–1;

4)  a₀+a₁z^–2.

89

Линейной дискретной цепи, имеющей структурную схему

соответствует сигнал на выходе Y(z)

1)  a₀+a₁z^–1X(z);

2)  a₀X(z)+a₁z^–1X(z);

3)  a₀z^–1X(z)+a₁X(z);

4)  a₀X(z)–a₁z^–1X(z).

90

Линейной дискретной цепи, имеющей структурную схему

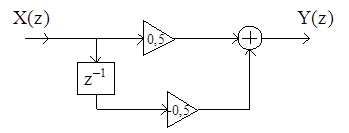
соответствует передаточная функция H(z)

1)  0,5+0,5·z^–1;

2)  0.5·z^–1–0,5·z¹;

3)  0.5·z^–1+0,5·z¹;

4)  0.5–0,5·z^–1.

91

Линейной дискретной цепи, имеющей структурную схему

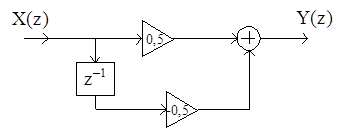
соответствует сигнал на выходе Y(z), равный

1)  0,5–0,5z^–1X(z);

2)  0,5X(z)–0,5z^–1X(z);

3)  0,5X(z)+0,5z^–1X(z);

4)  0,5z^–1X(z)–0,5X(z).