Математика \ Математические основы цифровой обработки сигнала

Теорема дискретной свертки. Число отсчетов импульсной характеристики дискретной цепи. Импульсная характеристика аналоговой цепи, страница 2

56

Если число отсчетов периодического сигнала x(nT) равно N за период, то число отсчетов Ck ДПФ будет равно

1)  N–1;

2)  N;

3)  N+1;

4)  2N.

57

Спектр Ck дискретного периодического сигнала задан N отсчетами. Число отсчетов дискретного сигнала x(nT) за период TC равен

1)  N–1;

2)  N;

3)  N+1;

4)  2N.

58

Отсчеты спектра дискретного периодического сигнала Ck для ДПФ определяются выражением

1)  Ck=;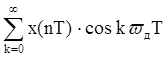

2)  Ck=;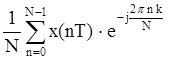

3)  Ck=;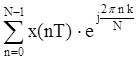

4)  Ck=.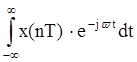

59

Если известны отсчеты C0,C1,…,CN–1 спектра дискретного периодического сигнала x(nT), то отсчеты самого сигнала определяются, как

1)  x(nT)= ;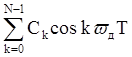

2)  x(nT)= ;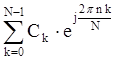

3)  x(nT)= ;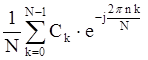

4)  x(nT)=.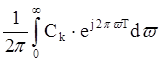

60

Прямое дискретное преобразование Фурье позволяет найти

1)  отсчеты дискретного сигнала x(nT);

2)  отсчеты спектра дискретного сигнала Ck;

3)  интервал дискретизации;

4)  период повторения спектра сигнала.

61

Обратное дискретное преобразование Фурье позволяет найти

1)  отсчеты дискретного сигнала x(nT);

2)  отсчеты спектра дискретного сигнала Ck;

3)  интервал дискретизации;

4)  период повторения спектра сигнала.


62

Для периодического дискретного сигнала x(nT)

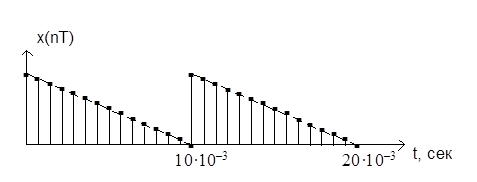
частота дискретизации спектра F при дискретном преобразовании Фурье равна

1)  0,1 кГц;

2)  1 кГц;

3)  0,2 кГц;

4)  2 кГц.

63

Частота дискретизации F спектра сигнала в дискретном преобразовании Фурье равна

1)  частоте дискретизации сигнала fд;

2)  верхней частоте спектра исходного аналогового сигнала Fв;

3)  удвоенной частоте спектра исходного аналогового сигнала 2Fв;

4)  величине, обратной периоду повторения дискретного сигнала 1/Tс.

64

Если спектр прямого дискретного преобразования Фурье имеет вид

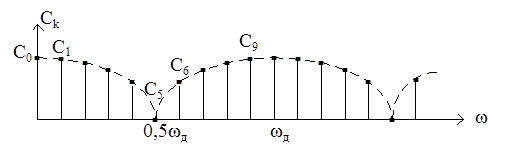
то число отсчетов дискретного сигнала x(nT) за период равно

1)  5;

2)  6;

3)  9;

4)  ?10.

65

Если частота дискретизации дискретного периодического сигнала x(nT), заданного  N отсчетами за период сигнала равна fд, то частота дискретизации F спектра ДПФ равна

1)  fд;

2)  2fд;

3)  fд/N;

4)  N· fд.

66

Если дискретный сигнал x(nT) задан N отсчетами за период сигнала TC, то частота дискретизации спектра сигнала F ДПФ равна

1)  1/NTC;

2)  1/TC;

3)  N/TC;

4)  2/TC.

67

Число отсчетов Ck={C0,C1,…} дискретного преобразования Фурье сигнала за период дискретизации ωд x(n)={x0,x1,…,xN–1} равно

1)  N–1;

2)  N;

3)  N+1;

4)  2N.

68

Для дискретной последовательности x(nT)={1;1;0}

Z–преобразование X(z) равно

1)  1+z–1;

2)  –1+z–2;

3)  1–z–1+z–2;

4)  z–1–z–2.

69

Для дискретной последовательности

x(nT)={–1;0;1} Z–преобразование X(z) равно

1)  1+z–1;

2)  –1+z–2;

3)  1–z–1+z–2;

4)  z–1–z–2.

70

Для дискретной последовательности

x(nT)={1;–1;1} Z–преобразование X(z) равно

1)  1+z–1;

2)  –1+z–2;

3)  1–z–1+z–2;

4)  z–1–z–2.

71

Для дискретной последовательности x(nT)={0;1;–1} Z–преобразование X(z) равно

1)  1+z–1;

2)  –1+z–2;

3)  1–z–1+z–2;

4)  z–1–z–2.

72

Z–преобразование X(z) дискретного сигнала x(n)=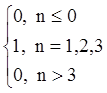равно

1)  1+z–1+z–2+z–3;

2)  z–1+z–2+z–3;

3)  1+z–1+z–2;

4)  1–z–1–z–2.

74

Z–преобразование  X(z)  дискретного  экспоненциального  сигнала x(nT)= =e–α·nT равно

Скачать файл