ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ
Хабаровский институт инфокоммуникаций (филиал)
Сибирский государственный университет
телекоммуникаций и информатики
Методическая разработка
по теме «Числовые и степенные ряды»
Хабаровск 2006
В методической разработке по теме «Числовые и степенные ряды» изложены основные процессы теории числовых и степенных рядов. Даны определения, формулировки теорем. Некоторые теоремы приведены с доказательством. Изложение сопровождается подробно разработанными примерами. В конце каждой главы даны упражнения.
Методическая разработка в помощь студентам – заочникам Хабаровского института инфокоммуникаций при изучении данной темы.
Составители: доктор ф – м. н., профессор ,
Ст. преподаватель .
1. ЧИСЛОВЫЕ РЯДЫ
1.1 Определение ряда и его суммы. Свойства рядов. Необходимый признак сходимости. Геометрический ряд и гармонический ряд
Пусть задана
последовательность чисел ![]() Для
любого конечного набора чисел
Для
любого конечного набора чисел ![]() можно
подсчитать следующую сумму
можно
подсчитать следующую сумму ![]() .
Если же взять всю последовательность и составить бесконечную сумму слагаемых,
то есть
.
Если же взять всю последовательность и составить бесконечную сумму слагаемых,
то есть ![]() ,
то получим новый объект, так как не умеем находить сумму бесконечного числа
слагаемых.
,
то получим новый объект, так как не умеем находить сумму бесконечного числа
слагаемых.
Определение 1. Выражение вида 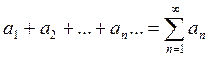 ,
где
,
где ![]() -
заданные числа, называется числовым рядом.
-
заданные числа, называется числовым рядом.
Числа ![]() называются
членами ряда;
называются
членами ряда; ![]() -
nй член ряда называется общим членом
ряда.
-
nй член ряда называется общим членом
ряда.
Очевидно, что для задания ряда нужно знать формулу общего члена ряда или по указанному закону составить формулу общего члена ряда.
Определение 2.
Сумма n первых членов ряда называется n-й частичной (частной) суммой ряда и
обозначается через Sn, то есть ![]() .
.
Определение 3. Предел n-ой частной суммы ряда, если он
существует и конечен, называется суммой ряда, то есть ![]() .
В этом случае числовой ряд называется сходящимся. Если
.
В этом случае числовой ряд называется сходящимся. Если ![]() или
не существует, то ряд называется расходящимся.
или
не существует, то ряд называется расходящимся.
Пример 1. Найти сумму ряда.
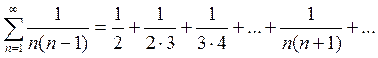
Заметим, что имеет место расположение
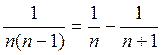 , тогда Sn перепишется в виде
, тогда Sn перепишется в виде
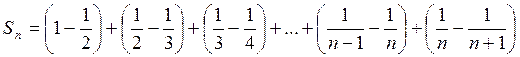 , отсюда
, отсюда 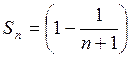 и
и
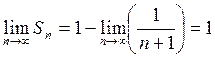 ,
то есть ряд сходится и его сумма равна 1.
,
то есть ряд сходится и его сумма равна 1.
Определение 4. Ряд вида 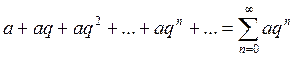 называется
геометрическим рядом.
называется
геометрическим рядом.
Теорема 1. Геометрический ряд сходится
при ![]() и
его сумма S равна
и
его сумма S равна 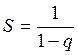 и
расходится при
и
расходится при ![]() .
.
Доказательство.
Приведем его толь для ![]() .
Нетрудно видеть, что n-ая частичная сумма имеет вид
.
Нетрудно видеть, что n-ая частичная сумма имеет вид
![]() (1)
(1)
Умножая на q равенство (1), получаем
![]() (2)
(2)
Из равенства (1)
вычитаем (2), получаем ![]() ,
отсюда
,
отсюда
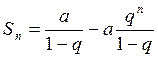 (3)
(3)
Известно, что при
![]() ,
,
![]() поэтому,
поэтому,
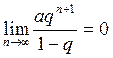 .
Тогда отсюда и из (3) вытекает равенство
.
Тогда отсюда и из (3) вытекает равенство 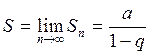 .
.
Для сходящихся числовых рядов имеют место следующие свойства:
Свойство 1. Отбрасывание любого конечного числа членов ряда не влияет на его сходимость.
Свойство 2. Если
члены сходящегося ряда 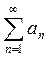 ,
имеющего сумму S, умножить на число λ, то
полученный ряд
,
имеющего сумму S, умножить на число λ, то
полученный ряд 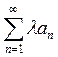 будет
также сходящимся, а число S - его
суммой.
будет
также сходящимся, а число S - его
суммой.
Свойство 3. Если
ряды 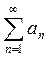 и
и
![]() сходятся,
то сходится и ряд
сходятся,
то сходится и ряд 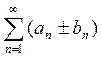 ,
причем его сумма равна алгебраической сумме исходных рядов.
,
причем его сумма равна алгебраической сумме исходных рядов.
Теорема 2. (Необходимый признак
сходимости). Если ряд 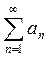 сходится,
то общий член данного ряда стремится к нулю при
сходится,
то общий член данного ряда стремится к нулю при ![]() ,
то есть
,
то есть ![]() .
.
Доказательство.
Согласно определению 2 n-ая и (n - 1)-ая частичные суммы данного ряда
имеют вид ![]() ,
,
![]() .
Так как ряд сходится, то
.
Так как ряд сходится, то ![]() ,
,
![]() .
Очевидно, что
.
Очевидно, что ![]() ,
поэтому
,
поэтому ![]() .
.
Следствие 1. Если
![]() ,
то ряд (1) расходится.
,
то ряд (1) расходится.
Например,
рассмотрим ряд 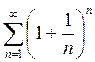 .
Здесь
.
Здесь 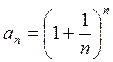 и
и
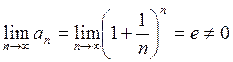 ,
значит ряд расходится.
,
значит ряд расходится.
Определение. Ряд
вида 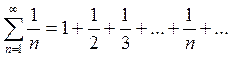 называется
гармоническим рядом.
называется
гармоническим рядом.
Теорема 3. Гармонический ряд
расходится. Доказательство данного факта приведем позже. У гармонического ряда 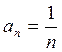 и
и
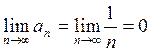 ,
а ряд тем не менее, расходится.
,
а ряд тем не менее, расходится.
1.2 Ряды с положительными членами. Признаки сходимости, признаки сравнения, признаки Даламбера и Коши, интегральный признак
Определение 1.
Ряд 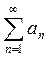 ,
члены которого неотрицательные числа, называется знакоположительным рядом.
,
члены которого неотрицательные числа, называется знакоположительным рядом.
Сформулируем ряд признаков, при помощи которых можно исследовать знакоположительные ряды на сходимость.
Напомним следующие факты:
Определение 2. Последовательность ![]() называется
неубывающей, если для всех n
выполнено неравенство
называется
неубывающей, если для всех n
выполнено неравенство ![]() .
.
Определение 3. Последовательность ![]() называется
ограниченной, если существует число М>0, не зависящее от n, такое, что
называется
ограниченной, если существует число М>0, не зависящее от n, такое, что ![]() .
.
Теорема А. Любая неубывающая, ограниченная последовательность имеет конечный предел.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.