Числовые и степенные ряды. Определение ряда и его суммы. Свойства рядов. Необходимый признак сходимости. Геометрический ряд и гармонический ряд, страница 2

Теорема (первый признак сравнения). Пусть даны ряды

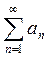   (1),    (2), причем для всех достаточно больших n выполняется неравенство . Тогда из сходимости ряда (2) следует сходимость ряда (1), из расходимости ряда (1) следует расходимость ряда (2).

Доказательство только в предположении, что ряд (2) сходится и неравенство (3) выполнено для всех n. Рассмотрим n-ые частичные суммы рядов (1) и (2).

,

Из (3) следует, что А_n  В_n. Очевидно, что последовательность частичных сумм  не убывает, так как . Ряд (2) сходится, то, по определению, существует конечный предел . В этом случае, как известно, последовательность В_n ограничена, то есть . Отсюда и из неравенства А_n  В_n следует, что последовательность А_n ограничена, то есть . Итак последовательность А_n неубывающая и ограничена. Следовательно, оп теореме А она сходится, то есть , где А – конечное число. Последнее означает, что ряд (1) сходится.

Теорема (второй признак сравнения). Рассмотрим два ряда (1) и (2). Если существует конечный, отличный от нуля предел 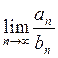, то оба ряда сходятся или расходятся одновременно.

В практических приложениях удобнее пользоваться вторым признаком.

Пример 1. Исследовать на сходимость ряд .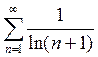

Решение. Общий член ряда 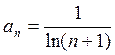. Сравним его с рядом . Известно, что , отсюда 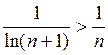. Так ряд  гармонический и он расходится, то по первому признаку расходится и исследуемый ряд.

Пример 2. Исследовать на сходимость ряд .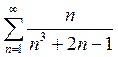

Решение. Общий член данного ряда 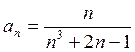. Рассмотрим ряд , где 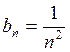(*). В дальнейшем будет показано, что ряд (*) сходится. Применим к данным рядам второй признак сравнения. Имеем 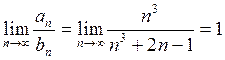. Тогда по второму признаку сравнения исследуемый ряд сходится.

Теорема (признак Даламбера). Пусть для членов ряда (1) выполняется условие

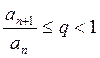                                                                                                       (4)

Тогда ряд сходится. Если же 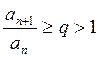, то ряд расходится.

Доказательство приведем для случая, когда выполнено условие (4). Из неравенства (4) имеем

                                                                                                         (5)

Применяя неравенство (5) последовательно получаем

Выделим неравенство

                                                                                                        (6)

Ряд 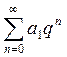 - геометрический с 0<q<1, он сходится. Тогда отсюда и из (6), согласно первого признака сравнения ряд (1) также сходится.

Для практических приложений удобнее использовать предельный признак Даламбера, который формулируется следующим образом:

Теорема: Дан ряд (1). Пусть члены этого ряда такие, что существует предел:

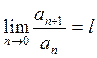
Тогда   1. при l< 1 ряд сходится;

2. при l > 1 ряд расходится;

3. при l = 1 признак неприменим.

Пример 1. Исследовать на сходимость ряд .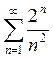

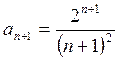Решение. Воспользуемся признаком Даламбера. Имеем , тогда . Найдем

.

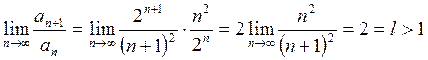Следовательно ряд расходится.

Пример 2. Исследовать на сходимость ряд .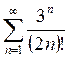

Решение. Применим признак Даламбера. Имеем 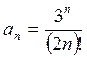, тогда 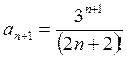. Найдем предел

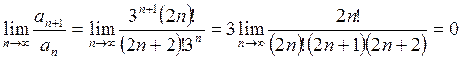
Следовательно, ряд расходится.

Здесь , .

Теорема (признак Коши). Дан ряд (1). Пусть члены этого ряда такие, что существует предел: . Тогда

1. При l< 1 ряд сходится;

2. При l > 1 ряд расходится;

3. При l = 1 признак неприменим.

Пример 3. Исследовать на сходимость ряд .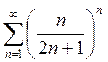

Решение. Применим признак Коши. Найдем

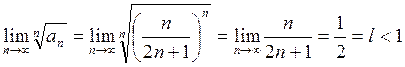
Следовательно, ряд сходится, согласно признака Коши.

Теорема (интегральный признак Коши). Дан ряд (1). Пусть неотрицательная на (1, ∞) функция f(x) монотонно убывает на (1, ∞) и такая, что, при целых n=1,2… f(n)=а_n. Тогда данный ряд и несобственный интеграл 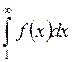 сходятся и расходятся одновременно.

Определение. Ряд вида , где p>0, называется обобщенным гармоническим рядом.

Теорема. Обобщенный гармонический ряд сходится при 0 < p < 1 и расходится при p > 1.

Доказательство. Примем интегральный признак. Общий член данного ряда . Тогда в качестве функции f(x) нужно взять функцию . Вычислим интеграл

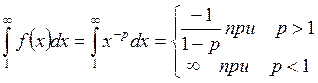
Таким образом, при p > 1 интеграл и ряд сходится, при 0 < p < 1 интеграл и ряд расходится.

При p = 1 имеем гармонический ряд, для которого 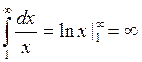 расходится. Следовательно, гармонический ряд расходится.

Пример. Исследовать на сходимость ряд .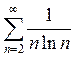

Решение. Примем интегральный признак. Рассмотрим функцию 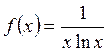 и вычислим интеграл 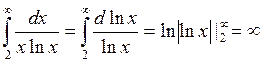. Интеграл расходится, следовательно и ряд расходится.

1.3 Знакочередующиеся ряды. Теорема Лейбница

Определение. Ряд вида