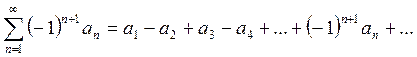 (1)
(1)
где an – положительные заданные числа, называется знакочередующимся.
Теорема
Лейбница.
Пусть члены знакочередующегося ряда (1) убывают, то есть ![]() общий
член аn стремится к нулю. Тогда
знакочередующийся ряд (1) сходится и для его суммы S имеет место оценка S≤а1.
общий
член аn стремится к нулю. Тогда
знакочередующийся ряд (1) сходится и для его суммы S имеет место оценка S≤а1.
Пример.
Исследовать на сходимость ряд 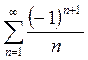 .
.
Решение. Применим
к заданному ряду теорему Лейбница. Члены ряда 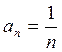 ,
,
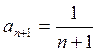 .
Отсюда
.
Отсюда ![]() и
и
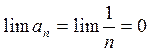 .
Следовательно, ряд сходится.
.
Следовательно, ряд сходится.
В приложениях
иногда возникает необходимость найти сумму S сходящегося ряда ![]() Допустим,
что ряд сходится, но сумму найти точно невозможно. Тогда естественно в качестве
приближенного значения S взять n-ю частную сумму:
Допустим,
что ряд сходится, но сумму найти точно невозможно. Тогда естественно в качестве
приближенного значения S взять n-ю частную сумму: ![]() .
Разность
.
Разность ![]() назовем
погрешностью вычисления.
назовем
погрешностью вычисления.
Величина Rn равна ![]() Это
есть знакочередующийся ряд. Для суммы
Это
есть знакочередующийся ряд. Для суммы ![]() ,
по теореме Лейбница, имеет место оценка
,
по теореме Лейбница, имеет место оценка ![]() .
Таким образом, если заменить сумму знакочередующегося ряда его частной суммой,
то погрешность вычисления будет не больше первого отброшенного члена ряда.
.
Таким образом, если заменить сумму знакочередующегося ряда его частной суммой,
то погрешность вычисления будет не больше первого отброшенного члена ряда.
Рассмотрим
знакочередующийся ряд ![]() и
ряд его абсолютных величин его членов
и
ряд его абсолютных величин его членов ![]()
Определение. Если сходится ряд из абсолютных величин членов знакочередующегося ряда, то знакочередующийся ряд называется абсолютно сходящимся.
Теорема. Если сходится ряд из абсолютных величин членов знакочередующегося ряда, то данный знакочередующийся ряд также сходится.
Пример. Исследовать на сходимость ряд
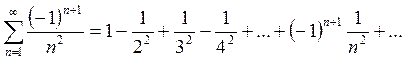
Решение. Составим
ряд из абсолютных величин членов данного ряда 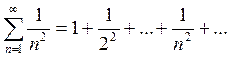 Это
обобщенный гармонический ряд с показателем р=2>1 он сходится. Значит
знакочередующийся ряд сходится абсолютно.
Это
обобщенный гармонический ряд с показателем р=2>1 он сходится. Значит
знакочередующийся ряд сходится абсолютно.
Определение. Если ряд из абсолютных величин членов знакочередующего ряда расходится, а данный знакочередующийся ряд сходится, то говорят, что знакочередующийся ряд сходится условно.
Пример. Исследовать на сходимость ряд
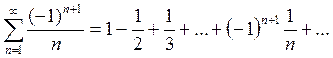
Решение. Составим ряд из абсолютных
величин членов данного ряда 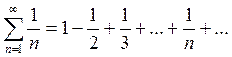 Это
ряд – гармонический. Он расходится. Исходный ряд, как было показано выше,
сходится. Следовательно, по определению исследуемый ряд сходится условно.
Это
ряд – гармонический. Он расходится. Исходный ряд, как было показано выше,
сходится. Следовательно, по определению исследуемый ряд сходится условно.
Упражнения.
Исследовать на сходимость следующие ряды:
|
1. 2. 3. 4. 5. |
6. 7. 8. 9. 10. |
2 ФУНКЦИОНАЛЬНЫЕ РЯДЫ
2.1 Функциональный ряд. Область сходимости. Теорема о дифференцируемости и интегрируемости ряда
В предыдущей главе мы рассматривали ряды, членами которых были постоянные величины. Возникает вопрос, можно ли рассматривать ряды, членами которых являются функции. В этом случае возникает новый объект исследования.
Определение 1. Ряд вида:
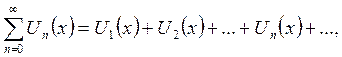 (1)
(1)
где Un(x) – заданные функции, определенные на одном и том же множестве Д, называется функциональным рядом.
Если подставить в
ряд (1) определенные числовые значения ![]() Д,
то будут получаться различные часовые ряды, среди которых могут оказаться как
сходящиеся, так и расходящиеся.
Д,
то будут получаться различные часовые ряды, среди которых могут оказаться как
сходящиеся, так и расходящиеся.
Определение 2.
Функциональный
ряд (1) сходится в точке х0![]() Д,
если сходится числовой ряд
Д,
если сходится числовой ряд 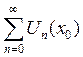 .
.
Определение 3.
Множество
всех значений х![]() Д,
для которых функциональный ряд (1) сходится, называется областью сходимости
функционального ряда (1).
Д,
для которых функциональный ряд (1) сходится, называется областью сходимости
функционального ряда (1).
Пусть х0
принадлежит области сходимости функционального ряда (1). Тогда функциональный
ряд (1) сходится в точке х0, то есть сходится числовой ряд 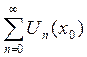 .
Выбирая различные значения х0 из области сходимости, мы будем
получать ряды, суммы которых зависят от х0. Следовательно, суммы
функционального ряда есть функция от переменной х.
.
Выбирая различные значения х0 из области сходимости, мы будем
получать ряды, суммы которых зависят от х0. Следовательно, суммы
функционального ряда есть функция от переменной х.
Рассмотрим ряд (1), где Un(x) определены и непрерывны на [a,b].
Определение 4. Будем говорить, что ряд (1)
мажорируется на [a,b] числовым рядом 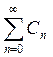 ,
если
,
если ![]()
![]() и
ряд
и
ряд 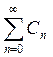 сходится.
сходится.
Теорема об
интегрируемости. Если ряд (1), Un(x) определены и непрерывны на [a,b] мажорируется, то ряд (1) можно
почленно интегрировать на [a,b], то есть имеет место неравенство  .
.
Теорема дифференцируемости. Пусть выполнены условия:
1. Функции Un(x) непрерывны и дифференцируемы на [a,b].
2. Ряд (1)
сходится на [a,b], а ряд 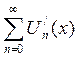 мажорируется
на [a,b] числовым рядом. Тогда
функциональный ряд (1) можно почленно дифференцировать, то есть
мажорируется
на [a,b] числовым рядом. Тогда
функциональный ряд (1) можно почленно дифференцировать, то есть 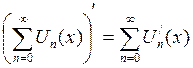 .
.
2.2 Степенные ряды. Теорема Абеля. Радиус сходимости
Определение 1. Степенными рядами называются ряды вида:
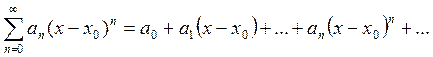 (1)
(1)
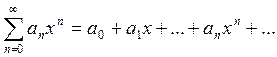 (2)
(2)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.