Теорема Абеля. Если степенной ряд (2)
сходится в точке х0, то он сходится для всех значений х,
удовлетворяющих неравенству ![]() .
Если же степенной ряд (2) расходится в точке x0, то он расходится для всех значений x, для которых
.
Если же степенной ряд (2) расходится в точке x0, то он расходится для всех значений x, для которых ![]() .
.
Из теоремы Абеля следует, что существует интервал (-R;R) во всех точках которого ряд (2) сходится и вне которого ряд (2) расходится. Этот интервал называется интервалом сходимости степенного ряда, а число R – радиусом сходимости степенного ряда.
Радиус сходимости степенного ряда можно вычислить по одной из формул:
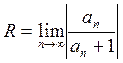 ,
,
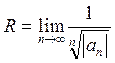
Пример 1. Найти
интервал сходимости степенного ряда 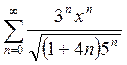 .
.
Решение. Здесь 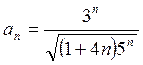 ,
,
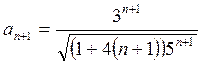 .
Воспользуемся формулой
.
Воспользуемся формулой 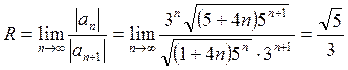 .
Итак, ряд сходится на интервале
.
Итак, ряд сходится на интервале 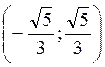 .
.
Пример 2. Найти
интервал сходимости степенного ряда 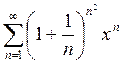 .
.
Решение.
Воспользуемся формулой 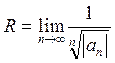 ,
здесь
,
здесь 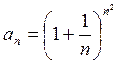 ,
получим
,
получим 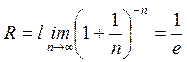 .
Следовательно, ряд сходится в интервале
.
Следовательно, ряд сходится в интервале 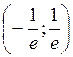 .
.
2.3 Ряды Тейлора и Маклорена. Разложение в ряд некоторых элементарных функций
Пусть функция f(x) определена и бесконечно дифференцируема в окрестности точки х0.
Определение 1. Ряд вида
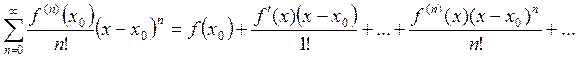 (1)
(1)
называется рядом
Тейлора функции ![]() в
точке х0.
в
точке х0.
Если х0=0, то ряд вида
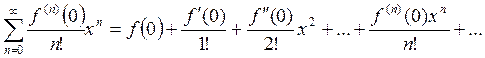 (2)
(2)
называется рядом
Маклорена функции![]() .
.
Пусть функция ![]() бесконечно
дифференцируема в окрестности точки х0. Составим ряд Тейлора (1) для
этой функции.
бесконечно
дифференцируема в окрестности точки х0. Составим ряд Тейлора (1) для
этой функции.
Вообще говоря,
если ряд (1) сходится, то его сумма S(x) не обязана совпадать с
функцией ![]() .
.
Укажем условия при выполнении которых сумма ряда Тейлора S(x) совпадает с функцией по которой построен данный ряд. В этом случае говорят, что функция раскладывается в ряд Тейлора.
Теорема. Если функция ![]() имеет
в некотором промежутке
имеет
в некотором промежутке ![]() производные
всех порядков, ограниченные одним и тем же числом M>0, то есть если
производные
всех порядков, ограниченные одним и тем же числом M>0, то есть если ![]() при
любом
при
любом ![]() ,
то функция
,
то функция ![]() в
каждой точке указанного промежутка разложима в ряд Тейлора.
в
каждой точке указанного промежутка разложима в ряд Тейлора.
Перейдем к разложению в ряд Маклорена некоторых элементарных функций.
1. Разложим
функцию ![]() =ех.
Для того, чтобы разложить ее в ряд Маклорена найдем значения
=ех.
Для того, чтобы разложить ее в ряд Маклорена найдем значения ![]() и
всех ее производных при х = 0.
и
всех ее производных при х = 0.
![]() =ех,
=ех,
![]() =1
=1
![]() =ех,
=ех,
![]() =1
=1
![]() =ех,
=ех,
![]() =1
=1
Все производные ![]() =ех
равномерно ограничены на любом конечном интервале [a,b]. Действительно,
=ех
равномерно ограничены на любом конечном интервале [a,b]. Действительно, ![]() .
Тогда по теореме
.
Тогда по теореме ![]() =ех
раскладывается в ряд Маклорена вида
=ех
раскладывается в ряд Маклорена вида
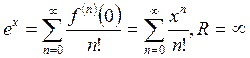 (3)
(3)
2. Аналогично
может быть получено разложение в ряд Маклорена следующих функций ![]() =cos x,
=cos x, ![]() =sin x,
=sin x,
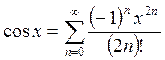 (4)
(4)
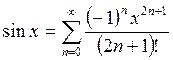 (5)
(5)
Радиусы сходимости R рядов (3), (4), (5) равны +∞.
Укажем теперь ряды Маклорена, которые сходятся на промежутке (-1;1). Ряд вида
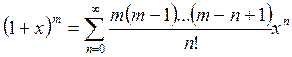 (6)
(6)
называется биномиальным.
При m=-1 из ряда (6) получаем:
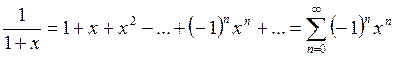 (7)
(7)
Интегрируя ряд (7) по х от 0 до t, где -1<t<1, получим
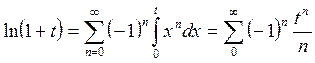 (8)
(8)
Положим в (7) x=t2 и проинтегрируем полученный ряд по t от 0 до х, -1<x<1, получим 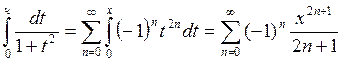 ,
итак
,
итак
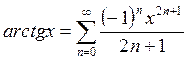 (9)
(9)
2.4 Применение рядов в приближенных вычислениях
Для того чтобы
найти приближенное значение функции ![]() можно
разложить эту функцию в ряд Маклорена и в качестве ее приближенного значения
взять частную сумму ряда.
можно
разложить эту функцию в ряд Маклорена и в качестве ее приближенного значения
взять частную сумму ряда.
Если функция раскладывается в знакочередующийся ряд, то погрешность вычисления будет не больше первого отброшенного ряда (см п.3).
Пример. Вычислить cos100 с точностью 10-4.
Решение.
Используем ряд (4) при 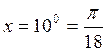 .
Найдем
.
Найдем 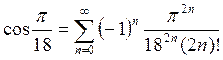 .
.
Можно вычислить,
что при n=2, 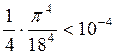 .
Поэтому остаток ряда, начиная с n=2, можно отбросить и с точностью до 10-4 имеем
.
Поэтому остаток ряда, начиная с n=2, можно отбросить и с точностью до 10-4 имеем 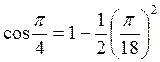 .
.
Аналогично можно использовать ряды для приближенного вычисления интегралов. Для этого подынтегральную функцию нужно разложить в ряд.
Пример. Вычисляем
интеграл 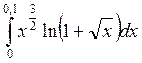 с
точностью до 10-4.
с
точностью до 10-4.
Решение.
Используем формулу (9) заменив t на ![]() :
:
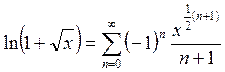 .
.
Тогда 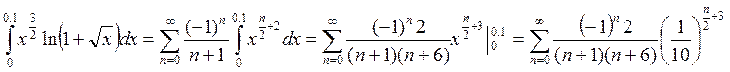
Очевидно, что n=2, а2=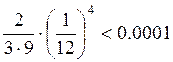 .
Тогда, отбросив остаток ряда, начиная с n=2, получим с точностью до 10-4
.
Тогда, отбросив остаток ряда, начиная с n=2, получим с точностью до 10-4 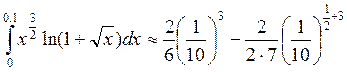 .
.
Упражнения а) Найти интервал сходимости степенного ряда
|
1.
2.
|
3.
4.
|
6.
6.
|
в) Вычислить с точностью до 0,001 следующие интегралы:
|
1.
2.
|
3.
4.
|
5.
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.