Методическая разработка по теории функций комплексных переменных.
Составитель: доцент
Комплексные числа и алгебраические действия над ними
1.1 Комплексные числа.
Определение 1. Комплексными числами
называются числа вида ![]() ,
где x и y – действительные числа, а
,
где x и y – действительные числа, а ![]() -
мнимая единица. Числа x и y называются соответственно
действительной и мнимой частями комплексного числа z и обозначаются
-
мнимая единица. Числа x и y называются соответственно
действительной и мнимой частями комплексного числа z и обозначаются
![]()
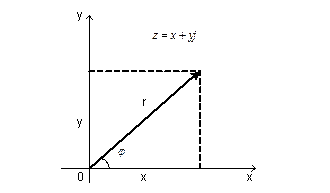 Рассмотрим комплексное число
Рассмотрим комплексное число ![]() и
будем трактовать x и y как
и
будем трактовать x и y как
координаты
точки на плоскости. Тогда каждому комплексному
числу ![]() будет
соответствовать точка (x, y) на плоскости. И обратно всякой точке
будет
соответствовать точка (x, y) на плоскости. И обратно всякой точке
(x, y) плоскости будет соответствовать определенное комплексное
число ![]() .
Кроме того, каждой точке
.
Кроме того, каждой точке ![]() можно
поставить в соответствие ее радиус – вектор. Плоскость XOY называется плоскостью комплексных
чисел или плоскостью z.
Действительные числа z=x изображаются точками на оси OX. Ось OX называется действительной осью.
можно
поставить в соответствие ее радиус – вектор. Плоскость XOY называется плоскостью комплексных
чисел или плоскостью z.
Действительные числа z=x изображаются точками на оси OX. Ось OX называется действительной осью.
Чисто мнимые числа z=yj изображаются точками на оси OY. Ось OY называется мнимой осью. Число![]() называется
бесконечно удаленной точкой. Множество, состоящее из всех конечных точек и
точки
называется
бесконечно удаленной точкой. Множество, состоящее из всех конечных точек и
точки ![]() ,
будем называть расширенной плоскостью z.
,
будем называть расширенной плоскостью z.
Определение 2. Два комплексных числа ![]() и
и
![]() называются
взаимно сопряженными.
называются
взаимно сопряженными.
Определение 3. Модулем комплексного числа ![]() называется
длина вектора z.
называется
длина вектора z.
Обозначим ![]() .
Из чертежа видно, что
.
Из чертежа видно, что ![]() .
.
Определение 4. Угол ![]() ,
образованный вектором z с положительным направлением
оси OX называется аргументом
комплексного числа z.
,
образованный вектором z с положительным направлением
оси OX называется аргументом
комплексного числа z.
Очевидно, что аргумент z имеет бесконечное число значений![]() .
Из чертежа следует, что
.
Из чертежа следует, что 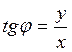 .
При z=0 функция Arg z не
определена. Из множества значений Arg z выделим так называемое главное значение аргумента,
которое лежит в интервале
.
При z=0 функция Arg z не
определена. Из множества значений Arg z выделим так называемое главное значение аргумента,
которое лежит в интервале ![]() и
обозначается arg z. Таки образом,
и
обозначается arg z. Таки образом, ![]() .
.
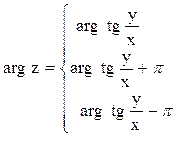 Главные значения аргумента
для различных точек z определяется из соотношений для точек Z из I и IY квадрантов;
Главные значения аргумента
для различных точек z определяется из соотношений для точек Z из I и IY квадрантов;
для точек Z из II квадранта;
для точек Z из III квадранта.
Очевидно, что ![]() .
Выражение вида
.
Выражение вида ![]() мы
будем называть алгебраической формой комплексного числа. Можно записать
комплексное число z и в других формах. Так
из чертежа следует, что
мы
будем называть алгебраической формой комплексного числа. Можно записать
комплексное число z и в других формах. Так
из чертежа следует, что ![]() .
Тогда
.
Тогда ![]() .
Мы получили тригонометрическую форму комплексного числа. По формуле Эйлера
.
Мы получили тригонометрическую форму комплексного числа. По формуле Эйлера ![]() .
Тогда
.
Тогда ![]() .
Это показательная форма комплексного числа.
.
Это показательная форма комплексного числа.
Пример. Представить в
тригонометрической и показательной формах комплексные числа ![]()
Решение. Для ![]() Тогда
Тогда
![]() ;
;
![]() -
действительное число, точка
-
действительное число, точка ![]() лежит
на оси OX, поэтому
лежит
на оси OX, поэтому ![]() .
Таким образом,
.
Таким образом, ![]() .
.
Число ![]() является
чисто мнимым, и точка
является
чисто мнимым, и точка ![]() лежит
на оси OY. Для всех чисто мнимых чисел
с отрицательной мнимой частью
лежит
на оси OY. Для всех чисто мнимых чисел
с отрицательной мнимой частью 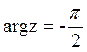 .
Итак,
.
Итак,
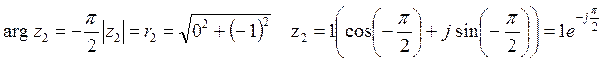 .
.
Для числа ![]() .
Точка
.
Точка ![]() лежит
в III четверти,
лежит
в III четверти, ![]() ,
поэтому
,
поэтому 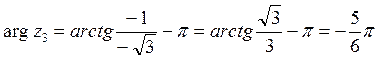 .
Таким образом
.
Таким образом 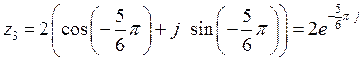 .
.
1.2 Действия над комплексными числами.
Два комплексных числа ![]() и
и
![]() равны
друг другу, если равны их вещественные и мнимые части
равны
друг другу, если равны их вещественные и мнимые части ![]() .
Суммой двух комплексных чисел
.
Суммой двух комплексных чисел ![]() и
и
![]() называется
комплексное число
называется
комплексное число ![]() .
Из определения вытекают законы сложения а) переместительный:
.
Из определения вытекают законы сложения а) переместительный: ![]() ;
;
б) сочетательный: ![]() .
.
Аналогично определяется разность комплексных чисел:
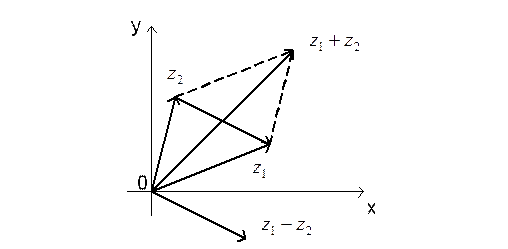
![]() .
.
Если воспользоваться правилами
сложения и вычитания векторов, то можно найти
точки на комплексной плоскости, соответствующие сумме комплексных чисел ![]() и
их разности
и
их разности ![]() .
.
Произведение ![]() комплексных
чисел
комплексных
чисел ![]() и
и
![]() определяется
равенством
определяется
равенством ![]() .
Здесь использован тот факт, что
.
Здесь использован тот факт, что ![]() .
Имеют место законы умножения:
.
Имеют место законы умножения:
а) переместительный ![]() ;
;
б) сочетательный ![]() ;
;
в) распределительный ![]() ;
;
Пусть числа ![]() и
и
![]() заданы
в показательной форме
заданы
в показательной форме ![]() ,
,
![]() .
.
Тогда ![]() .
Таким образом, модуль произведения комплексных чисел
.
Таким образом, модуль произведения комплексных чисел ![]() и
и
![]() равен
произведению их модулей
равен
произведению их модулей ![]() .
Аргумент произведения комплексных чисел
.
Аргумент произведения комплексных чисел ![]() и
и
![]() равен
сумме их аргументов
равен
сумме их аргументов ![]() .
.
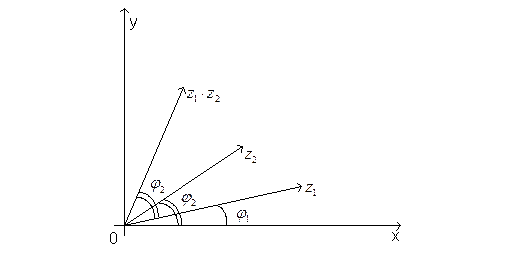 Отсюда следует, что при умножении
Отсюда следует, что при умножении ![]() на
на
![]() вектор
вектор
![]() растягивается
(сжимается) в
растягивается
(сжимается) в
![]() раз
и поворачивается на угол
раз
и поворачивается на угол ![]()
против часовой стрелки.
Число ![]() называется
частным чисел
называется
частным чисел ![]() и
и
![]() :
:
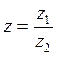 ,
если
,
если ![]() .
При
.
При ![]() частное
частное
![]() всегда
существует. Действительно, умножим равенство
всегда
существует. Действительно, умножим равенство ![]() на
на
![]() получим
получим
![]() .
Отсюда
.
Отсюда
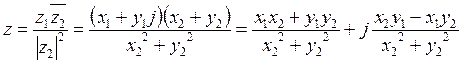 .
.
Пример. Найти частное 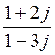 .
.
Решение: 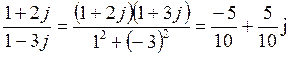
Пусть ![]() и
и
![]() выражены
в показательной форме
выражены
в показательной форме
![]() ,
,
![]() .
Тогда
.
Тогда 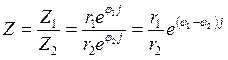 .
Следовательно, модуль частного комплексных чисел равен частному их модулей
.
Следовательно, модуль частного комплексных чисел равен частному их модулей
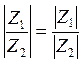 .
.
Аргумент частного комплексных чисел равен разности аргумента числителя и аргумента знаменателя
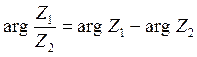 .
.
Рассмотрим комплексное число ![]() и
запишем его в показательной и тригонометрических формах
и
запишем его в показательной и тригонометрических формах
![]() .
.
Возведем Z в степень n, где n – целое число (положительное или
отрицательное). Получим ![]() .
В частности, при Z=1 получаем формулу Муавра
.
В частности, при Z=1 получаем формулу Муавра
![]() .
.
Пример. Вычислить ![]() .
.
Решение. Пусть Z=![]() .
Найдем
.
Найдем ![]() и
arg Z.
и
arg Z.
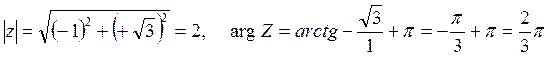 .
.
Тогда 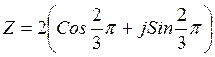 ;
;
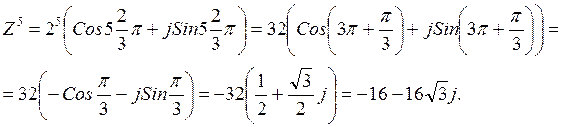
Число W
называется корнем натуральной степени n из числа Z ![]() ,
если
,
если ![]() .
Запишем Z в тригонометрической форме
.
Запишем Z в тригонометрической форме
![]() .
.
Тогда, так как ![]() ,
то получим
,
то получим
![]() .
.
Отсюда 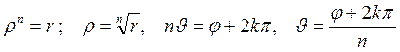
Следовательно, 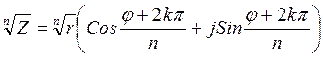 (1.1)
(1.1)
Уравнение ![]() имеет
n различных корней. Все
эти корни можно найти, если формуле (1.1) придать k значения 0, 1, 2, …, n-1.
имеет
n различных корней. Все
эти корни можно найти, если формуле (1.1) придать k значения 0, 1, 2, …, n-1.
Пример. Найти ![]() .
.
Решение. 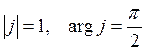 .
.
Тогда 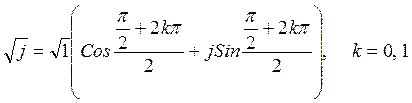 .
.
При k=0 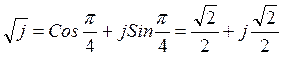
При k=1 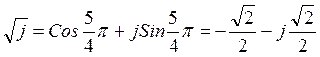 .
.
2. Основные понятия теории функций комплексного переменного
2.1 Области и их границы.
Определение 1. ![]() -
окрестностью точки
-
окрестностью точки ![]() называется
множество точек z, лежащих внутри круга с
центром точке
называется
множество точек z, лежащих внутри круга с
центром точке ![]() радиуса
радиуса
![]() ,
т. е. множество точек z, удовлетворяющих неравенству
,
т. е. множество точек z, удовлетворяющих неравенству
![]() .
.
Определение 2. Пусть нам дано множество E точек комплексной плоскости. Точка ![]() называется
внутренней для множества E, если вместе с точкой
называется
внутренней для множества E, если вместе с точкой
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.