Определим потери от быстронатекающей ползучести бетона ,для чего вычислим напряжение в бетоне в середине пролёта от действия силы P1 и изгибающего момента Mw от собственной массы плиты.
Нагрузка от собственной массы плиты равна:
![]()
Тогда:
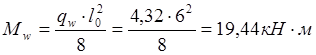
Напряжение
![]() на уровне растянутой
арматуры (т .е при
на уровне растянутой
арматуры (т .е при ![]()
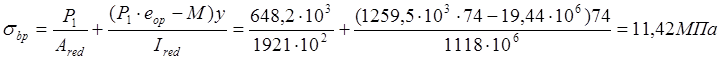
Назначаем
передаточную прочность бетона ![]()
![]() ,удовлетворяющий требованию
п.2.6 [11].
,удовлетворяющий требованию
п.2.6 [11].
Потери от быстронатекающей ползучести бетона будет равно:
- на уровне
растянутой арматуры при :![]() ,поскольку
,поскольку ![]() ,то:
,то:
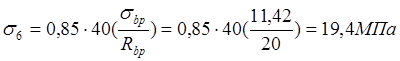
(здесь коэффициент 0,85 учитывает тепловую обработку при твердении бетона).
Первые потери:
![]()
Тогда усилие обжатие с учётом первой потери:
![]()
Определим максимальную сжимающее напряжение в бетоне от действия силы P без учёта собственной массы ,принимая y=y0=104мм:
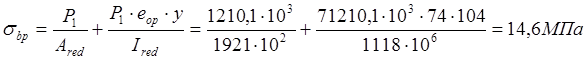
Поскольку ![]() ,то требование п.1.29 [11]
удовлетворяются.
,то требование п.1.29 [11]
удовлетворяются.
Определим вторые потери предварительно напряжения армирования по поз.8 и 9 таб.5[11].
Потери от усадки тяжёлого бетона:
![]()
Напряжение в бетоне от действия силы P1 и изгибающего момента Mw будет равно:
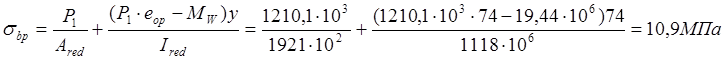
Поскольку ![]() ,то:
,то:
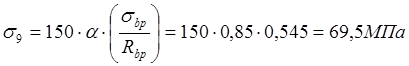
Итого вторые потери:
![]()
Суммарные потери:
![]()
(установленная минимальная величина потери предварительного напряжение), поэтому согласно п.1.25[11] потери не увеличиваем.
Усилие обжатие с учётом суммарных потерь и коэффициента точности натяжение арматуры будет равно:
![]()
Расчёт по образованию трещин производим из условия (124) [11]:
![]()
Согласно
п.4.5 [10],принимаем ![]()
Вычислим момент образованию трещин ![]() по методу ядровых моментов:
по методу ядровых моментов:
![]()
Момент сопротивление приведённого сечение для крайнего растянутого волокна с учётом неупругих деформаций растянутого бетона можно определить по формуле:
![]()
Расстояние от центра тяжести приведённого сечение до ядровой точки наиболее удалённой от растянутой зоны, вычислим по формуле (132)[11] :
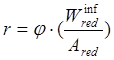
где 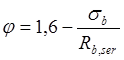 .
.
Так как при действии усилий обжатие P1,в стадии изготовление минимальное напряжение в бетоне (в верхней зоне)равное:
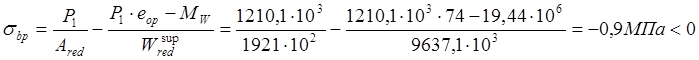
т .е будет сжимающим ,то верхние начальные трещины не образуются.
При действии внешние нагрузки в стадии эксплуатации,максимальное напряжение в сжатом бетоне:
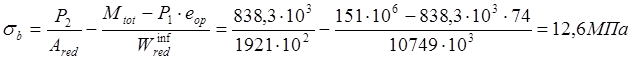
Вычислим 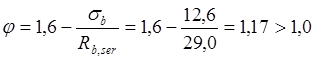 ,согласно п.4.5[11],принимаем соответсвенно
,согласно п.4.5[11],принимаем соответсвенно ![]() .Тогда :
.Тогда :
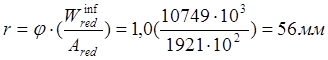
![]()
![]()
Расчёт по раскрытию трещин нормальных к продольной оси плиты, выполняем в соответствии с п.4.14 и п.4.15[11].Вычисляем дополнительные геометрические характеристики и расчётные коэффициенты для приведённого сечение, необходимые для расчёта по раскрытию трещин,согласно п.4.28[11].
При не продолжительном действии полной нагрузки M=Mtot=151кН∙м,
Ntot=P2=838,3кН
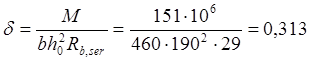
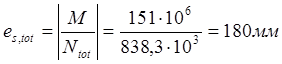
![]() ,
,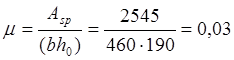 ;
;![]()
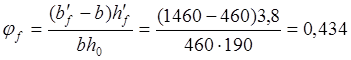
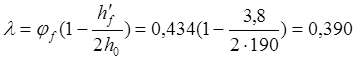
тогда
при ![]() (для тяжёлого бетона),получим:
(для тяжёлого бетона),получим:
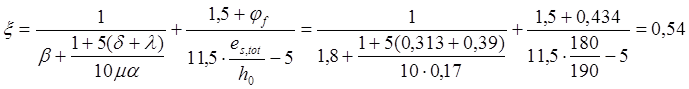
![]()
Следовательно ,плечо внутренний пары сил при непродолжительном действии нагрузок будет равно:
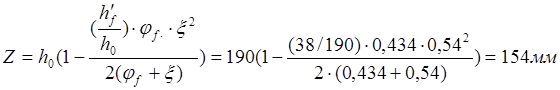
При продолжительном действии постоянной и длительной нагрузки M=M1=138кН,получим соответственно:
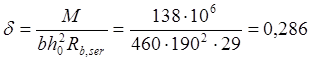
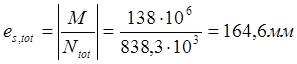
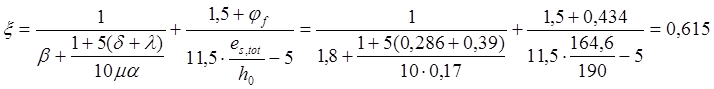
![]()
Следовательно , плечо внутренний пары сил при продолжительном действии нагрузок будет равно:
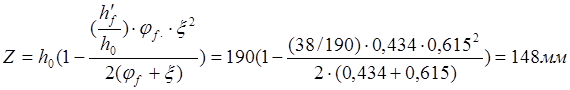
Приращение напряжений в растянутой арматуре от непродолжительного действия полной нагрузки(M=Mtot=151кН∙м,Z=154мм).
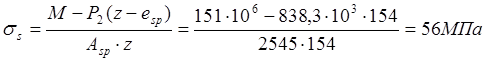
(esp=0,так как усилия обжатия приложено в центр тяжести напрягаемой арматуры).Тоже ,от непродолжительного действия постоянной и длительной нагрузок при M=M1=138кН∙м.
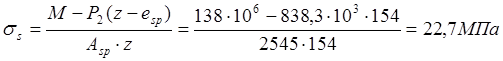
То же,от продолжительного действия постоянной и длительной нагрузок при Z=148мм:
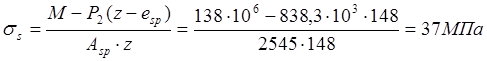
Ширину раскрытий трещин от непродолжительного действия полной нагрузки вычисляем по формуле (144)[11]:
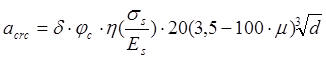
где ![]() ;для арматуры периодического профиля
;для арматуры периодического профиля ![]() -диаметр продольной арматуры.
-диаметр продольной арматуры.
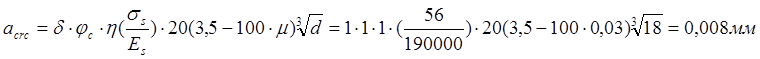
то же ,от непродолжительного действия постоянной и длительной нагрузок:
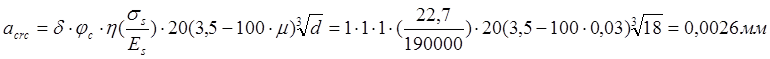
То же от продолжительного действия постоянной и длительной нагрузок:
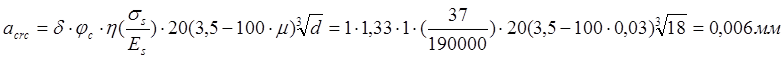
Ширина непродолжительного раскрытия трещин составит:
![]() а,ширина
продолжительного раскрытия трещин составит:
а,ширина
продолжительного раскрытия трещин составит:
![]()
Следовательно ,требование к плите по трещиностойкости удовлетворяется.
Расчёт прогиба плиты.
Расчёт прогиба плиты выполняем согласно пп 4.27-4.30[10] при условии наличие трещин в растянутой зоне бетона.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.