Расчет и конструирование несущих железобетонных и каменных конструкций многоэтажного здания (плиты, ригеля, колонны, фундамента, простенка, стены подвала), страница 4

(e_sp=0,так как усилия обжатия приложено в центр тяжести напрягаемой арматуры).Тоже ,от непродолжительного действия постоянной и длительной нагрузок при M=M₁=138кН∙м.

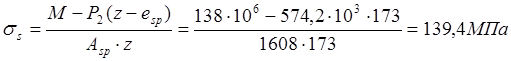
То же,от продолжительного действия постоянной и длительной нагрузок при  Z=171мм:

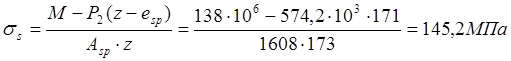
Ширину раскрытий трещин от непродолжительного действия полной нагрузки вычисляем по формуле (144)[11]:

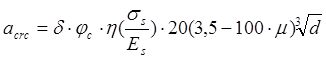
где  ;для арматуры периодического профиля -диаметр продольной арматуры.

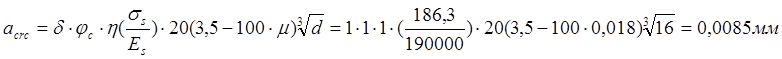
то же ,от непродолжительного действия постоянной и длительной нагрузок:

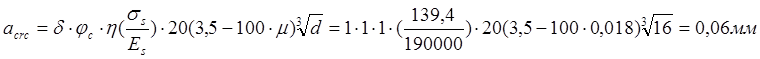
То же от продолжительного действия  постоянной и длительной нагрузок:

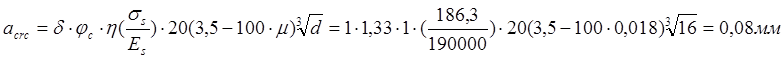
Ширина непродолжительного раскрытия трещин составит:

а,ширина продолжительного раскрытия трещин составит:

Следовательно ,требование к плите по трещиностойкости  удовлетворяется.

Расчёт прогиба плиты.

Расчёт прогиба плиты выполняем согласно пп 4.27-4.30[11] при условии наличие трещин в растянутой зоне бетона.

Вычисляем кривизну предварительно напряжённого изгибаемого элемента от непродолжительного действия полной нагрузки .Для этого определяем значение коэффициента ,для чего по формуле (168) [11] находим коэффициент  ,принимая  M_r=M_tot=151 кН∙м.

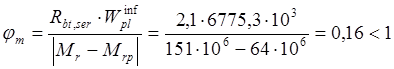
Согласно таб.36 [11] принимаем ,для арматуры периодического профиля и бетона классов выше В7,5.Поскольку:

принимаем

Тогда по формуле (167)[11] получим:

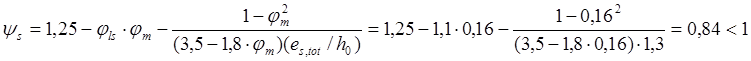
Согласно п.4.27 и таб.35[11] принимаем .

Кривизну от непродолжительного действия полной нагрузки ,вычисляемая по формуле(160) [11],будет равна:

∙

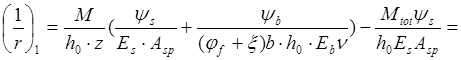
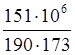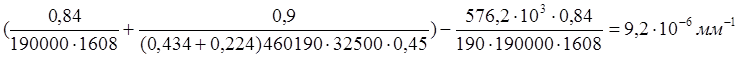
Вычислим кривизну от непродолжительного действия постоянных и длительных нагрузок. Определим значение коэффициента ,принимая значение M_r=M₁=138кН∙м:

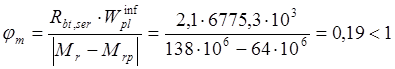
Согласно таб.36 [11] принимаем ,для арматуры периодического профиля и бетона классов выше В7,5.Поскольку:

принимаем  

Тогда по формуле (167)[11] получим:

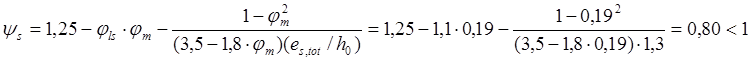
Принимаем .Согласно п.4.27 и таб.35[11],принимае

Кривизну от непродолжительного действия постоянной и длительной нагрузок ,вычисляемая по формуле (160)[11]:

∙

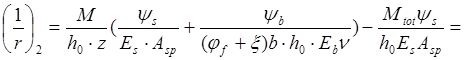
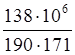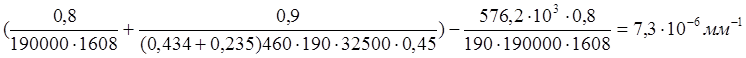
Вычислим кривизну от продолжительного действия постоянных и длительных нагрузок.

Согласно таб.36 [11] принимаем ,для арматуры периодического профиля и бетона классов выше В7,5.Поскольку:

принимаем 

Тогда по формуле (167)[11] получим:

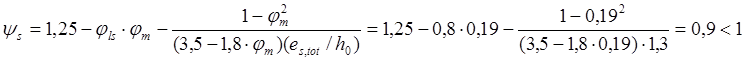
Согласно п.4.27 и таб.35[11],  принимаем

Кривизну от продолжительного действия постоянной и длительной нагрузки , вычислим по формуле (160)[11]:

∙

 

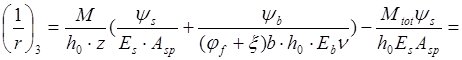
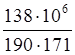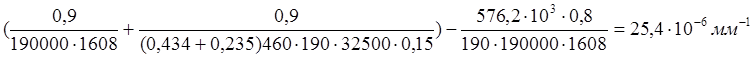
Выгиб плиты в следствии усадки и ползучести бетона от усилия предварительного обжатия по формуле (158)[11]:

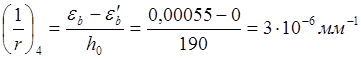
где 

Полная кривизна участка плиты с трещинами в растянутой зоне определяется по формуле  (170)[11]:

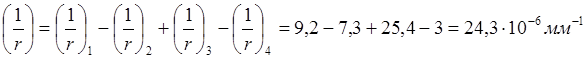
Вычисляем прогиб по формуле:

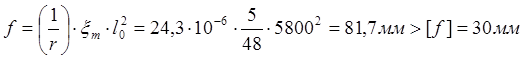
следовательно , не удовлетворяется требование по деформациям.

Для выполнения этого условия необходимо увеличить площадь предварительно-напряжённой арматуры:

Для обеспечение требований по прогибу принимаем :

 

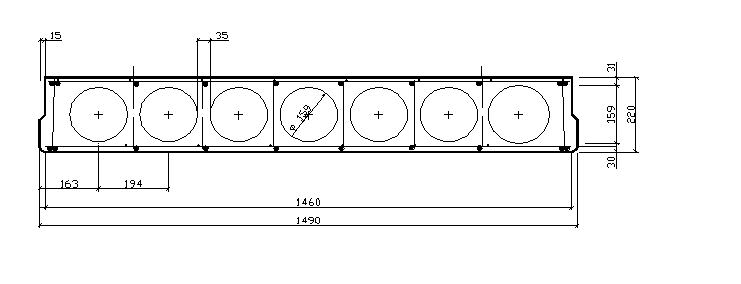
Определим геометрические характеристики приведённого сечение.

Площадь приведённого сечение:

Статический момент приведённого сечение относительно оси, прохдящей по нижней грани плиты.

          Статический момент приведённого сечение относительно оси, прохдящей по нижней грани плиты.

Расстояние от нижней грани до центра тяжести приведённого сечение:

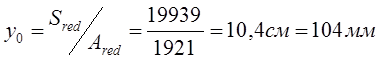
Момент инерции приведённого сечение:

Момент сопротивление приведённого сечение по нижней зоне:

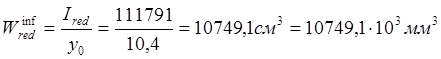
Момент сопротивление приведённого сечение по верхней зоне:

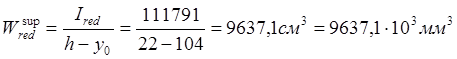
Расчёт потери  предварительного  напряжение.

Определим первые потери предварительного напряжение напрягаемой арматуры по поз. 1-6 таб. 5 [11]

-потери от релаксации напряжение в арматуре:

-потери от температурного перепада:

Так как при пропаривании форм с упорами вместе нагревается и изделие.

-потери от деформации анкеров в виде инвентарных зажимов:

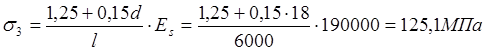
-потери от деформации стальной формы:

Таким образом ,усилие обжатие  P₁ ,с учётом потери по поз. 1-5 таб.5[11] равно:

Точка приложение усилий  P₁ совпадает с центром тяжести сечение напряжённой арматуры ,поэтому: