При статистическом (пассивном) методе
используются данные об изменениях входных ![]() и выходных
и выходных ![]() переменных
объекта, которые представляют собой случайные величины. Определение статических
характеристик при этом сводится к нахождению связи между случайными величинами
и к оценке достоверности этой связи. Статистический метод базируется на
принципах теории вероятности и математической статистики.
переменных
объекта, которые представляют собой случайные величины. Определение статических
характеристик при этом сводится к нахождению связи между случайными величинами
и к оценке достоверности этой связи. Статистический метод базируется на
принципах теории вероятности и математической статистики.
Математическая статистика представляет
собой науку описания и анализа статистических экспериментальных данных,
получаемых в результате наблюдения. Она базируется на теории вероятностей. Так
как в процессе опыта получают ограниченный объем значений, наблюдаемых величии,
то характеристики случайных величин и систем случайных величин, вычисленные по
этим данным, сами являются величинами случайными. Их значения зависят от объема
полученных экспериментальных данных. Эти значения называют оценками
соответствующих характеристик, например, оценка математического ожидания ![]() , дисперсии
, дисперсии ![]() , коэффициента
корреляции
, коэффициента
корреляции ![]() , корреляционного отношения
, корреляционного отношения
![]() . Будем использовать
выражения оценок, удовлетворяющих требуемым свойствам состоятельности,
несмещенности и эффективности. В дальнейшем под названием характеристик
случайных величин и систем случайных величин будем подразумевать их оценки.
. Будем использовать
выражения оценок, удовлетворяющих требуемым свойствам состоятельности,
несмещенности и эффективности. В дальнейшем под названием характеристик
случайных величин и систем случайных величин будем подразумевать их оценки.
Имеется технологический объект
(промышленный аппарат, лабораторная установка и т.п.), у которого
контролируемыми являются: выходная величина ![]() , определяющая результат
функционирования объекта, например, расход целевого продукта, концентрация
целевого компонента в продуктовом потоке, селективность процесса, температура в
контролируемой точке и т.п.; входные величины
, определяющая результат
функционирования объекта, например, расход целевого продукта, концентрация
целевого компонента в продуктовом потоке, селективность процесса, температура в
контролируемой точке и т.п.; входные величины ![]() ,
, ![]() ,...,
,..., ![]() , определяющие значения
расходов поступающих в объект материальных или энергетических потоков, состав
исходной смеси, её температура и т.п. или промежуточные контролируемые
параметры, влияющие на значение выходной величины.
, определяющие значения
расходов поступающих в объект материальных или энергетических потоков, состав
исходной смеси, её температура и т.п. или промежуточные контролируемые
параметры, влияющие на значение выходной величины.
Выходные и входные величины объекта являются случайными, поскольку на них, как правило, действуют не контролируемые параметры, изменяющиеся случайным образом. Поэтому уравнения, составленные для случайных величин, отражают не истинную, а статистическую, или стохастическую, связь.
Требуется определить такой вид функциональной зависимости (уравнение регрессии)
![]() (3.18)
(3.18)
и такие значения её коэффициентов, при
которых соотношение (3.18) адекватно исследуемому объекту в диапазоне изменения
его параметров. Под адекватностью понимается совпадение с определенной точностью
результатов расчета выходной величины ![]() по соотношению (3.18) к
ее экспериментальным значениям
по соотношению (3.18) к
ее экспериментальным значениям ![]() при
одних и тех же значениях входных параметров. Решение задачи включает следующие
этапы.
при
одних и тех же значениях входных параметров. Решение задачи включает следующие
этапы.
1. Оценка линейной статистической связи между величинами объекта и определение коэффициентов линейного уравнения регрессии.
2. Оценка нелинейной статистической связи между величинами объекта и определение коэффициентов нелинейного уравнения регрессии.
Если нет предварительных данных о характере связи между выходной и входными величинами объекта, форму уравнения регрессии (3.18) выбирают линейной:
![]() (3.19)
(3.19)
Пусть имеется таблица значений наблюдаемых входных и выходной величины (табл.3.1).
Таблица 3.1. Значения наблюдаемых величин
|
Переменные |
Номер опытов |
1 |
2 |
3 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
|
… |
… |
… |
… |
… |
… |
||
|
… |
… |
... |
… |
… |
… |
... |
|
|
|
|
|
|
... |
|
|
|
|
|
|
|
|
… |
|
|
Теснота
линейной связи между выходной и входными величинами оценивается коэффициентом
множественной корреляции ![]() .
.
Полная сумма квадратов отклонений выходной величины относительно её среднего определяется выражением
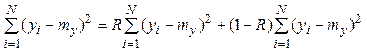 , (3.20)
, (3.20)
где составляющая 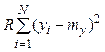 обусловлена разбросом
значений выходной величины
обусловлена разбросом
значений выходной величины ![]() ,
вычисленных по (3.19), относительно среднего
,
вычисленных по (3.19), относительно среднего ![]() , а
, а 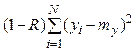 обусловлена разбросом
экспериментальных значений выходной величины
обусловлена разбросом
экспериментальных значений выходной величины ![]() относительно уравнения
регрессии (3.19).
относительно уравнения
регрессии (3.19).
Таким образом, физически коэффициент
корреляции характеризует в изменении параметра ![]() ту долю, которая
вызвана пропорциональным действием контролируемых параметров. Чем выше значение
ту долю, которая
вызвана пропорциональным действием контролируемых параметров. Чем выше значение
![]() , тем точнее по уравнению (3.19) можно предсказать значение
, тем точнее по уравнению (3.19) можно предсказать значение ![]() . Значения
. Значения ![]() заключены
в пределах
заключены
в пределах ![]() .
Если
.
Если ![]() , то
связь (3.19) является функциональной. При
, то
связь (3.19) является функциональной. При ![]() , линейная зависимость
отсутствует.
, линейная зависимость
отсутствует.
Если ![]() , то имеет место более или менее тесная корреляционная связь. Для оценки
линейной связи между двумя случайными величинами используется коэффициент
парной корреляции
, то имеет место более или менее тесная корреляционная связь. Для оценки
линейной связи между двумя случайными величинами используется коэффициент
парной корреляции ![]() , который определяется по выражению:
, который определяется по выражению:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.