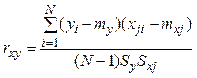 , (3.21)
, (3.21)
где 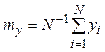 - среднее значение
(математическое ожидание) величины
- среднее значение
(математическое ожидание) величины ![]() ,
, 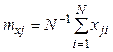 - среднее
значение величины
- среднее
значение величины ![]() ,
, 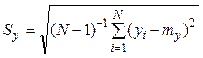 - среднеквадратичное
отклонение величины
- среднеквадратичное
отклонение величины ![]() ,
, 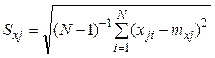 - среднеквадратичное
отклонение величины
- среднеквадратичное
отклонение величины ![]() ;
;![]() -
число наблюдений.
-
число наблюдений.
Коэффициент парной корреляции изменяется в
пределах ![]() .
.
Чем больше входных переменных в уравнении
(3.19), тем выше значение ![]() , т.к. при этом выходная величина описывается
более полно. Использование коэффициента корреляции как меры тесноты связи
обосновано лишь в том случае, когда исследуемые случайные переменные имеют нормальные
многомерные распределения. В противном случае интерпретация
, т.к. при этом выходная величина описывается
более полно. Использование коэффициента корреляции как меры тесноты связи
обосновано лишь в том случае, когда исследуемые случайные переменные имеют нормальные
многомерные распределения. В противном случае интерпретация ![]() не
надежна. Линейные уравнения вида (3.19), как правило, удовлетворяют условию
нормального многомерного распределения [1]. Приведем переменные
не
надежна. Линейные уравнения вида (3.19), как правило, удовлетворяют условию
нормального многомерного распределения [1]. Приведем переменные ![]() к нормированному виду
по формулам
к нормированному виду
по формулам
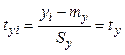 (3.22)
(3.22)
и
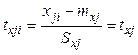 , (3.23)
, (3.23)
где ![]() обладает следующим
свойством:
обладает следующим
свойством:
![]() ; (3.24)
; (3.24)
![]() . (3.25)
. (3.25)
Покажем это:
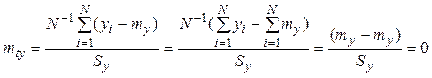 ,
,
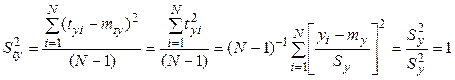 .
.
Запишем выражения коэффициентов парной корреляции между нормированными переменными с учетом (3.24) и (3.25):
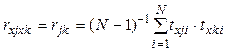 , (3.26)
, (3.26)
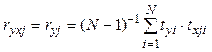 . (3.27)
. (3.27)
Выразим ![]() и
и ![]() из (3.22) и (3.23) и подставим в (3.19). При
условии, что
из (3.22) и (3.23) и подставим в (3.19). При
условии, что 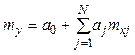 , получим
, получим
![]() , (3.28)
, (3.28)
где
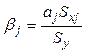 ,
, ![]() . (3.29)
. (3.29)
Для определения коэффициентов ![]() воспользуемся методом
наименьших квадратов. Составим функцию рассогласования (невязки) экспериментальных
воспользуемся методом
наименьших квадратов. Составим функцию рассогласования (невязки) экспериментальных
![]() и
рассчитанных
и
рассчитанных ![]() по
уравнению (3.28) нормированных значений выходной величины:
по
уравнению (3.28) нормированных значений выходной величины:
 , (3.30)
, (3.30)
Подставим выражение (3.28) в (3.30)и,
используя необходимые условия минимума функции ![]()
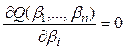 ,
, ![]() , получим систему уравнений:
, получим систему уравнений:
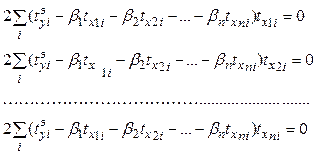 . (3.31)
. (3.31)
Раскроем скобки в системе уравнений (3.31),
разделим все члены на ![]() и, используя
выражения (3.26) и (3.27), получим систему нормальных уравнений:
и, используя
выражения (3.26) и (3.27), получим систему нормальных уравнений:
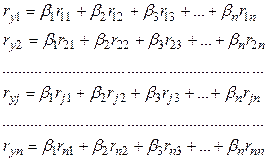 . (3.32)
. (3.32)
Перепишем систему уравнений (3.32) в матричной форме:
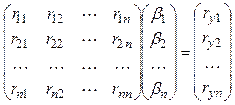 (3.33)
(3.33)
Введем обозначения:
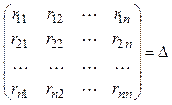 ; (3.34)
; (3.34)
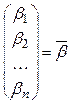 ; (3.35)
; (3.35)
 . (3.36)
. (3.36)
С учетом обозначений (3.34), (3.35), и (3.36), уравнение (3,33) примет вид
![]() . (3.37)
. (3.37)
Умножим обе части равенства (3.37) слева на матрицу (3.38), обратную матрице (3.34):
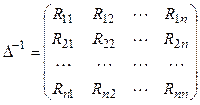 , (3.38)
, (3.38)
![]() . (3.39)
. (3.39)
Учитывая, что ![]() - единичная матрица,
уравнение (3.39) примет вид
- единичная матрица,
уравнение (3.39) примет вид
![]() . (3.40)
. (3.40)
Подставляя в (3.40) выражения (3.38) и (3.36), получим
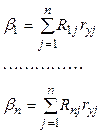 . (3.41)
. (3.41)
По найденным значениям ![]() и
элементам
и
элементам ![]() матрицы (3.34),
матрицы (3.34), ![]() ,
вычисляется коэффициент множественной корреляции
,
вычисляется коэффициент множественной корреляции
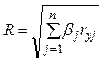 (3.42)
(3.42)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.