Исследование статики объекта методом пассивного эксперимента. Определение вида уравнения регрессии и вычисление его коэффициентов, страница 4

Наиболее распространен полиномиальный вид нелинейного уравнения регрессии:

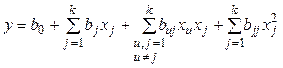.                                 (3.48)

Нелинейные члены в уравнение (3.48) вводят по результатам оценки тесноты нелинейной связи между входными  и выходной  величинами, которая определяется корреляционным отношением  по формуле:

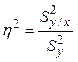,                                                                                     (3.49)

где  - дисперсия линии регрессии относительно математического ожидания выходной величины;  - дисперсия выходной величины относительно математического ожидания.

Для иллюстрации определения оценки корреляционного отношения воспользуемся рис. 3.1.

Рис. 3.1. К определению корреляционного отношения

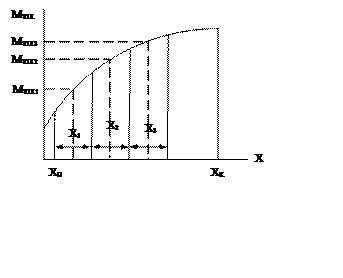Для определения величины  ось  разобьем на  равных интервалов. В каждом интервале определим математическое ожидание величины  и отнесем его к значению , определяющему середину соответствующего интервала, т.е.

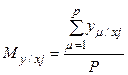,                                                                        где  - значение выходной величины  в -ом интервале величины ,  - число наблюдений в -ом интервале. Теперь величину  можно определить как

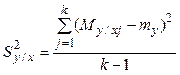,                                                           где

.                                                                                   

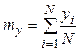Величина  определяется по формуле:

.                                                                      

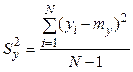Для оценки значимости коэффициентов корреляции  и корреляционных отношений  пользуются  - критерием. Коэффициент корреляции  признается незначимым, если выполняется условие [4]:

,                                                        где индексы  и () определяют числа степеней свободы  и .

Для корреляционного отношения условие незначимости имеет вид

.                                         

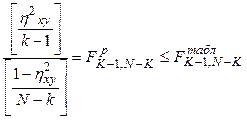Для значимых коэффициентов корреляции проверяется гипотеза о линейности регрессии по  - критерию. Регрессия признается линейной, если выполняется условие:

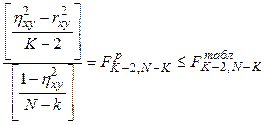.                       (3.50)

Если найдены коэффициенты корреляции  и корреляционные отношения  между выходной и входной величинами, а также коэффициенты корреляции  и корреляционные отношения  между входными величинами, то вид уравнения (3.48) для химико-технологических процессов можно конкретизировать, используя следующие рекомендации:

-  если  значим для возмущающих воздействий и , то в уравнение вводится только одно из них, например ;

-  если  значим для управляющего воздействия  и возмущающего воздействия , то в уравнение вводится член в виде , а если при этом и , и  - расходы, то в уравнение вводят член ;

-  если значимы и близки коэффициент корреляции  и корреляционное отношение , т.е. выполняется условие (2.46), то величина  вводится в уравнение регрессии в линейном виде ;

-  если значимы и , и , но условие (3.50) не выполняется, то величина  вводится в уравнение регрессии и в линейном, и в квадратичном виде ( и ).

Для определения коэффициентов нелинейного уравнения регрессии пользуются методом наименьших квадратов. Произведения и квадраты параметров, входящих в уравнение (3.48), назовем групповыми случайными переменными. Если групповые случайные переменные имеют нормальное распределение, то уравнение регрессии (3.48) через групповые случайные переменные можно записать в виде линейного уравнения (3.19). Для определения его коэффициентов в этом случае можно воспользоваться изложенным выше методом определения коэффициентов линейного уравнения регрессии.