Исследование статики объекта методом пассивного эксперимента. Определение вида уравнения регрессии и вычисление его коэффициентов, страница 3

При выборках небольшого объема величину  корректируют [1] по формуле

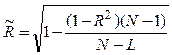,                                                                          (3.43)

где  - число коэффициентов исходного уравнения регрессии. В рассматриваемом случае . Для практического использования уравнения (3.28) переходят к исходному выражению (3.19).При этом, пользуясь формулами (3.22) , (3.23) для выражения переменных и и формулой (3.29) для выражения коэффициентов , как

.                                                                                                  

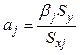Коэффициент  выражают из очевидного условия 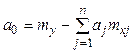. При слабой корреляции между входными параметрами, т.е. при , система уравнений (3.32) принимает вид

.                                                                                          

С другой стороны, если между входными величинами, например  и  имеет место сильная корреляция, соответствующие строки системы уравнений (3.32) будут пропорциональны и одна из них не будет нести дополнительной информации. В этом случае одну из входных переменных  или  нужно из уравнения регрессии (3.19) исключить. Следует также отметить, что с вычислительной точки зрения наличие пропорциональности между  и  вызывает трудности при решении системы нормальных уравнений (3.32) в связи с плохой её обусловленностью (главный определитель системы при этом близок к нулю).

После определения коэффициентов , , проверяетсяих значимость для  по критерию Стьюдента. С этой целью определяют величину :

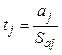,                                                                                                        где  - среднеквадратичное отклонение коэффициента регрессии .  вычисляется по формуле

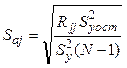,                                                                                       где  - диагональный элемент матрицы (3.38),  - дисперсия выходной величины относительно среднего значения,  - дисперсия выходной величины относительно уравнения регрессии.

Коэффициент уравнения регрессии  признается значимым, если выполняется условие

,                                                                                      где  - табличное значение  с  степенями свободы для заданного уровня значимости  и т.д.

Незначимые коэффициенты  из уравнения регрессии исключают. Затем проверяется адекватность уравнения регрессии по критерию Фишера. Вычисляется величина

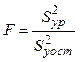,                                                                     (3.44)

где  - дисперсия уравнения регрессии относительно среднего значения . Она определяется с учётом (3.20) по выражению

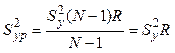,                                                            (3.45)

где  - сумма квадратов отклонений уравнения регрессии от среднего значения,  - коэффициент множественной корреляции, вычисленный по выражению (3.42) или (3.43),  определяется по выражению

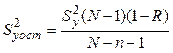.                                                             (3.46)

Подставляя (3.45) и (3.46) в (3.44), получим

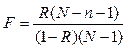.                                                                        (3.47)

Вычисленное по (3.47) значение  сравнивается с табличным значением , взятым при заданном уровне значимости  и т.д. для числа степеней свободы  и .  принимается для дисперсии , а  - для дисперсии .

При условии , уравнение регрессии (3.19 ) считается адекватным объекту. Чем больше  по сравнению с , тем эффективнее уравнение регрессии. Если указанное условие не выполняется, то выходную величину нужно описывать нелинейным уравнением регрессии.

3.2.1.2. Определение нелинейной стохастической связи между величинами объекта и вычисление коэффициентов нелинейного уравнения регрессии