Построение и анализ эффективности инвестиционных стратегий для финансовых рынков на основе простой регрессионной модели, страница 5

Предполагает, что шум  является “белым” гауссовским, то есть, центрированным и с независимыми значениями. В этом случае получаемые оценки коэффициентов обладают желательными свойствами оптимальности.

Для вывода оценок  коэффициентов a, b , c наиболее естественно применить метод наименьших квадратов в том виде, как он использовался в построении оценок коэффициентов двухфакторной линейной регрессии. Действительно, уравнения (  ) и (  ) формально совпадают при замене переменных

                                     ,                        (   )

так что оценки  для коэффициентов a, b , c ряда авторегрессии (  ) получаются из формул (  ) с учетом этих замен.

В качестве экспериментальной выборки (  ) теперь следует взять некоторый отрезок предыстории временного ряда . Обозначим длину этого интервала предыстории через T, то есть, в качестве экспериментальных наблюдений будет использоваться отрезок временного ряда

Оценки  коэффициентов, полученные по этой предыстории, соответствуют моменту времени t и их можно обозначить как . Формулы для вычисления оценок  получаются (  ) с учетом замен (  ):

                                                                            (  )

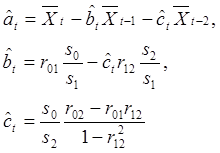Здесь индексы 0, 1, 2 обозначают сдвиг во времени назад от текущего момента t:

                                     (   )

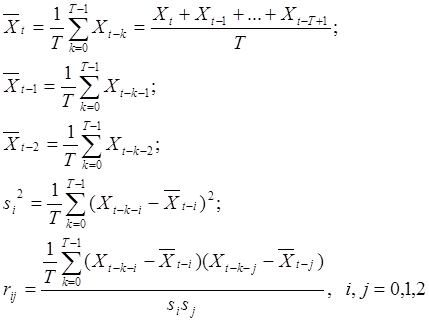Прогноз  будущего значения временного ряда, построенный на основе предыстории , получается при замене в формуле (  ) неизвестных коэффициентов a, b , c на их оценки (  ):

                                                                                      (  )

Таким образом, формула дает прогноз  будущего значения  временного ряда, вычисленный в момент времени t на основе имеющейся предыстории ряда , отсчитываемой назад от текущего момента t на глубину, определяемую заданной длиной предыстории Т.

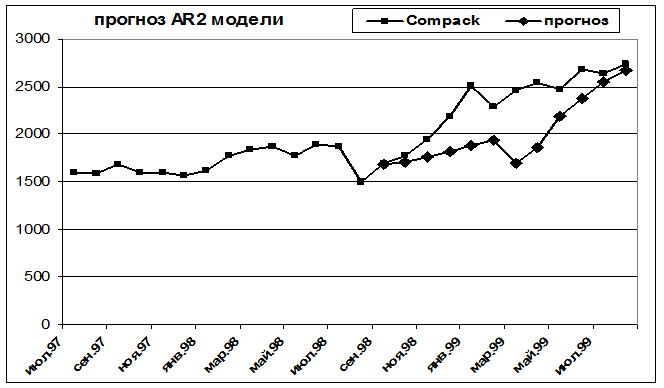
Рис. 2.2. Прогноз модели  для курса акций АО Compack

(Нью-Йоркская фондовая биржа)

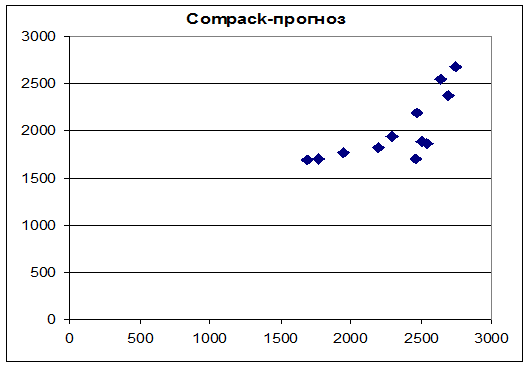
Рис. 2.3. Диаграмма рассеяния для реального курса акций Compack и прогноза

(средняя относительная ошибка прогноза 5,48 %)

На рисунках 2.2. и 2.3. приведены для иллюстрации результаты прогнозирования в соответствии с моделью ряда Юла, полученные для акций американской корпорации Compack на основе графика курса акций на Нью-Йоркская фондовой бирже.

Глава  3. Анализ прогнозов и эффективности

торговых систем для финансовых рынков

3.1. Моделирование и измерение эффективности

торговых систем: методика и экспериментальные результаты

Вопрос об измерении качества прогноза в применении к торговым системам является достаточно сложным и не исчерпывается только проблемой точности прогноза.

В обычной постановке задачи прогнозирования ищется наилучший прогноз в смысле наименьшего отклонения от наблюдаемой реализации. Однако, если учесть, что построенный прогноз используется затем в некоторой торговой системе, то понятие качества прогноза изменяется, поскольку наилучшим будет тот прогноз, который дает наибольшую прибыль.

И нетрудно привести соображения, показывающие, что наиболее прибыльным может оказаться прогноз, не обязательно имеющий высокую точность в смысле, скажем, СКО. Действительно, значения прогнозов используются в торговой системе существенно нелинейным образом, поскольку сама торговая система представляет собой весьма нелинейное по своей природе отображение графика в вещественную ось (нелинейный функционал). Например, если при открытии позиций используется главным образом направление изменения графика (а не абсолютная величина этого изменения) и построенный прогноз безошибочно предсказывает знак этого изменение (хотя и сильно ошибается в величине предсказанного изменения), то при использовании прогноза в торговой систем будет получен высокий результат, хотя по величине СКО данный прогноз будет хуже других.