Построение и анализ эффективности инвестиционных стратегий для финансовых рынков на основе простой регрессионной модели, страница 4

Уравнение (3) определяет модель наблюдения, соответствующую данному эксперименту. Значения “шума”обычно рассматриваются как последовательность независимых случайных величин. В классических моделях, изучаемых в математической статистике [   ] [   ],  имеют гауссовское распределение с нулевым математическим ожиданием и одинаковой дисперсией.

Для того чтобы на основе выборки  найти оценки  параметров a, b, c, используется метод наименьших квадратов [   ], в соответствии с которым необходимо минимизировать квадратичную форму

                               .                            (4)

Условие минимума функции , получаемое приравниванием к нулю частных производных от  по a, b и c , представляет собой систему линейных уравнений

                                                                      (4)

решение которой имеет вид

                                                                                               (   )

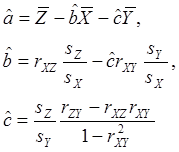где  - обозначают выборочные средние значения (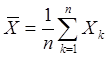 и аналогично для Y, Z),  - выборочные среднеквадратичные отклонения, определяемые соотношениями вида

 = , а  - попарные выборочные коэффициенты корреляции соответствующих переменных:

                      .                     ()

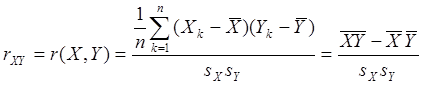Хорошо известны оптимальные свойства оценок , получаемых в методе наименьших квадратов: если шумы  являются центрированными (имеют нулевые математические ожидания, ) с одинаковыми дисперсиями и они некоррелированы ( ), то оценки  являются несмещенными (математические ожидания оценок  совпадают с истинными значениями параметров a, b , c) они имеют наименьшие дисперсии среди всех возможных линейных несмещенных оценок []   [].

Точность построенной аппроксимации зависимости  переменной Z от переменных X и Y определяется выборочным совокупным коэффициентом корреляции R,

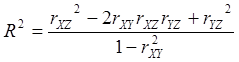
Коэффициент R подобно обычному коэффициенту корреляции принимает значения    [      ].

2.5. Прогнозирование временного ряда на основе линейной

модели авторегрессии второго порядка

Если наблюдения, получаемые в результате эксперимента, представляют собой последовательность измерений некоторой величины Х в моменты времени t= 0, 1, 2,…., то эти наблюдения составляют временной ряд и обозначаются  или очень часто применяется обозначение . Наблюдения в виде временных рядов широко применяются в различных экономических приложениях; временными рядами представляются валютные курсы, цены различных товаров, курсы акций, процентные ставки и т.д..

Важнейшей прикладной задачей является построение прогноза временного ряда. Общая формулировка задачи прогнозирования приведена в Приложении 1. В дипломной работе будет рассмотрена простая модель временного ряда (широко известный в эконометрике ряд Юла [  ]), на основе которой выведены оценки параметров и формулы для прогноза, примененные затем для построения инвестиционных стратегий.

Ряд Юла является моделью временного ряда, называемой авторегрессией второго порядка (и обозначаемой в литературе как ):

                                                ;                                                 (  )

таким образом, если принять, что время t измеряется днями, то соотношение (  ) означает, что будущее (завтрашнее) значение величины Х является линейной функцией от сегодняшнего и вчерашнего значений Х. Для реальных приложений это слишком упрощенная модель, но благодаря ее простоте она позволяет обнаружить важные свойства в динамике реальных наблюдений временных рядов и применить их для построения инвестиционных стратегий на финансовых рынках.

Коэффициенты a, b , c в модели (  ) неизвестны и должны быть оценены на основе имеющихся наблюдений. К уравнению (  ) необходимо добавить еще модель наблюдения, чтобы иметь возможность обосновать свойства получаемых оценок. Классическая модель наблюдений

                                                                                       (  )