Технико-экономические расчеты Гомельской дистанции пути, страница 6

μ и η - функции, учитывающие влияние соседних с расчетным колес, соответственно, на изменения изгибающего момента М_дин и поперечной силы Q_дин под расчетным колесом; определяются по следующим формулам:

μ = ƒ∙ (к_x) = е^-kx ∙ (cos kX - sin kX),

η = ƒ∙ (к_x) = е^-kx ∙ (cos kX - sin kX),

 (2.10)

В  формуле  (2.10)  коэффициент  относительной  жесткости  подрельсового основания и рельса соответственно для лета  к_л,  см^-1, и для зимы  к₃,  см^-1,

определяются по формуле (2.2).

В формуле (2.9) среднее квадратическое отклонение вертикальных сил S, кгс, определяется по формуле:

 (2.11)

где  S_p- среднее   квадратическое  отклонение  вертикальных  сил,  вызываемое

колебаниями рессор, кгс;

Sнп- среднее квадратическое отклонение вертикальной силы, вызываемое

неровностями на пути, определяется по формуле (2.7);

q₁- доля  колес  в  поезде,  имеющих  изолированные  неровности,  в  виду

отсутствия фактических данных принимается q₁ = 0,05;

S_инк и S_ннк- среднее квадратическое отклонение давления колеса на рельс, обусловленное силами инерции неподрессоренных масс, возникающих ответственно при наличии изолированной неровности на колесе и при наличии непрерывных плавных неровностей на колесах, кгс,

S_p = 0,08∙ Р_р                                                                          (2.12)

где  Р_р- максимальное значение вертикальных сил, вызываемых колебаниями рессор, кгс.

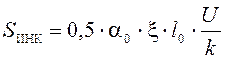                                                      (2.13)                                                         

где α₀= 0,433- для пути с деревянными шпалами;

ξ - максимальный дополнительный прогиб рельса при прохождении колесом синусоидальной неровности, принимается исходя из сопоставления рассматриваемой скорости движения поезда V, км/ч, с критической скоростью Vкр,км/ч.

ξ = 1,47, еслиV ≥ Vкр, где

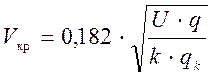                                                                   (2.14)

 в противном случае                                                                  

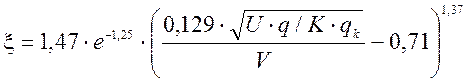(2.15)

где   g— ускорение силы тяжести g = 0,981см/с²;

е₀ - величина наибольшей расчетной глубины изолированной неровности на колесе, принимается равной две трети от предельно допустимой глубины ползуна   и   составляет   для   колес   локомотивов   0,047см   при   буксовых подшипниках качения. Среднее квадратическое отклонение S_инк, кгс, определяется по формуле:

                   (2.16)        

где  d- диаметр колеса по кругу катания. Изгибающий  момент   М_ДИН, кгс∙см,  действующий  на рельс  в расчетном сечении, и давление на шпалу Q_ДИН, кгс, в расчетном сечении определяются по следующим формулам:

М_дин = Р'_экв /4k;   М_дин = (k∙l/2)∙Р''_экв                                                                     (2.17)       

где  l -расстояние между осями шпал на прямом участке пути 1=55см.                                               Осевые напряжения на нижней постели подошвы рельса σ _П-О  кгс/см², и на верхней поверхности головки рельса σ_г-о кгс/см², от изгиба, кромочные напряжения в подошве σ_п-к кгс/см², и головке рельса σ_г-к  кгс/см², определяются по формулам:

σ_П-О = М_ДИН/W_п;    σ_г-о = М_ДИН/ W_г;

σ_п-к = f ∙ σ_П-О; σ_г-к= m_г-к ∙ σ_П-О,                                                                      (2.18)

где  W_п и W_г - момент сопротивления рельса относительно, соответственно, подошвы и головки при изгибе в вертикальной плоскости, согласно [1 приложение 5] для новых рельсов типа Р65 W_п =417см³ и W_г = 330см³;

f и m_г-к - соответственно коэффициенты перехода от осевых напряжений к

кромочным  в  подошве  и  головке рельса,  учитывающие  горизонтальный     прогиб и кручение рельса.

Средние   напряжения  в  балластном  слое  под   шпалами   в   подрельсовом сечении  σ_Б  кгс/см²,  и действующие  напряжения  под  подкладкой  в  шпалах

σ_Щ  кгс/см², определяются по следующим формулам:

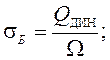
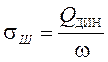                                                                                                                             (2.19)

   где  Ω - эффективная опорная площадь полушпалы. При щебеночном балласте и деревянных шпалах Ω = 2853 см², согласно [1, приложение 10].

ω -опорная  площадь  рельсовой  подкладки.  При  типе  промежуточного скрепления ДО и рельсах Р65 ω = 507см², согласно [1, приложение 11]. Напряжения    на    основной    площадке    земляного    полотна    σ_h  кгс/см²

определяются по формуле:

σ_h = σ'_h+ σ'_hc+ σ''_hc                                                                                     (2.20)     

где σ'_h - напряжение от воздействия расчетной шпалы на глубине h, см, от ее нижней постели, кгс/см²;

σ'_hc и σ''_hc - напряжения  соответственно  от  воздействия  первой  и  второй соседних с расчетной шпал, кгс/см².

σ'_h = r₁∙ σ_δ ∙ (0,635m∙ C₁+1,275∙ (2- m) ∙ C₂);

σ'_hc = (r₁/π) ∙A∙σ'_δc; σ''_hc = (r₁/π) ∙A∙σ''_δc;

C₁ = (b/2h)-(b³/24h³); C₂ = b∙h/b²+4h²; m = 8,9/σ_δ+4,35;                        (2.21)

A = β₁+0,5 ∙sin 2β₁- β₂- 0,5∙ sin 2β₂;

β₁ = arctg(l+0,5b)/h; β₂ = arctg(l- 0,5b)/h,

где σ_δ  - среднее давление на балласт в подрельсовом сечении расчетной шпалы,

определяется по формуле (2.19), кгс/см²;

r₁   -   поправочный   коэффициент,   для   пути   с   деревянными   шпалами

принимается равным 0,8;

b - ширина нижней постели шпалы, согласно. Для деревянных шпал b = 25 см;

h - толщина балластного  слоя от нижней  постели  шпалы до  основной

площадки, см;

β₁ и β₂  - углы между вертикалью и прямой, соединяющей начало и конец

полосовой нагрузки с точкой, в которой определяется напряжение, рад;