Расчет пространственного бруса.
Выполняем расчет пространственного бруса (рисунок 1, а). Средний элемент бруса имеет круглое сечение диаметром d, а два другие - прямоугольные с размерами b и h. Торец круглого элемента примыкает к большей стороне прямоугольного, причем d = h.
При выполнении расчета принимаем:
Р1 = 3qa, b = 0,045 м,
Р2 = 1,5qa, h = 0,11 м,
q = 47 кН/м , R = 210 Мпа,
a = 0,675 м.
Вычерчиваем пространственный брус в изометрии (рисунок 1, б).
Используя метод сечений, получаем значения внутренних силовых факторов в граничных сечениях 1 – 8 (рисунок 2)
|
Стержень 1 (рисунок 1а) |
||||||||||||||
|
N(1)= |
0 |
qa |
Qx(1)= |
0 |
qa |
Мк(1)= |
0 |
qa2 |
Мx(1)= |
0 |
qa2 |
|||
|
N(2)= |
0 |
qa |
Qx(2)= |
0 |
qa |
Мк(2)= |
0 |
qa2 |
Мx(2)= |
3 |
qa2 |
|||
|
Qy(1)= |
3 |
qa |
Мy(1)= |
0 |
qa2 |
|||||||||
|
Qy(2)= |
3 |
qa |
Мy(2)= |
0 |
qa2 |
|||||||||
|
Стержень 2 (рисунок 1б) |
||||||||||||||
|
N(3)= |
0 |
qa |
Qy(3)= |
1 |
qa |
Мк(3)= |
3 |
qa2 |
Мx(3)= |
0 |
qa2 |
|||
|
N(4)= |
0 |
qa |
Qy(4)= |
2 |
qa |
Мк(4)= |
3 |
qa2 |
Мx(4)= |
0.5 |
qa2 |
|||
|
Qx(3)= |
1 |
qa |
Мy(3)= |
0 |
qa2 |
|||||||||
|
Qx(4)= |
2 |
qa |
Мy(4)= |
3 |
qa2 |
|||||||||
|
Стержень 2 (рисунок 1б) |
||||||||||||||
|
N(5)= |
-3 |
qa |
Qy(5)= |
1.5 |
qa |
Мк(5)= |
0.5 |
qa2 |
Мx(5)= |
3 |
qa2 |
|||
|
N(6)= |
-3 |
qa |
Qy(6)= |
1.5 |
qa |
Мк(6)= |
0.5 |
qa2 |
Мx(6)= |
-1.5 |
qa2 |
|||
|
Мy(5)= |
0 |
qa2 |
||||||||||||
|
Мy(6)= |
0 |
qa2 |
||||||||||||
В соответствии с полученными значениями и принятыми правелами строим эпюры внутренних силовых факторов (рисунок 3, а-г). Правильность построения эпюр проверяем по равенству узлов (рисунок 3, д, е).
Расчет на прочность стержня 1.
Опасным сечением является сечение 2, так как в нем действует максимальный изгибающий момент. Вычерчиваем это сечение в рабочем положении с дейсвующими в нем внутренними силовыми факторами (рисунок 4), направление внутренних усилий берём из соответствующих эпюр.
|
Qx= |
0 |
кН |
Мх= |
0 |
кН*м |
|||
|
Qy= |
3qa= |
8.1 |
кН |
Му= |
3qa2= |
5.5 |
кН*м |
Геометрические характеристики рассматриваемого
сечения следующие:
|
Jx=bh3/12= |
499 |
*10-8 |
м4, |
|
|
Jy=hb3/12= |
84 |
*10-8 |
м4, |
|
|
S*x=bh/2*h/4=bh2/8= |
68 |
*10-8 |
м4, |
|
|
S*x=bh/2*b/4=hb2/8= |
28 |
*10-8 |
м4. |
|
Полные нормальные напряжения в опасном сечении определяются суммой напряжений от изгибающих моментов
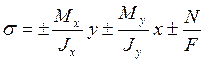 (1)
(1)
Знаки слогаемых в формуле выбираются по знаком отдельных напряжений в первом квадрате (рисунок 4) вдоль оси у - плюс, вдоль оси х - плюс.
Поэтому
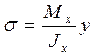 (2)
(2)
Уравнение нулевой линии получим, положив в формуле σ = 0:
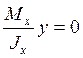 y
= 0
y
= 0
Нулевая линия проходит через центр тяжести сечения в первом и третьем квадратах (рисунок 5), с углом наклона к оси х:
Максимальное нормальное напряжение будет в точке А(-b/2,h/2). Поэтому в формуле (2) подставляем х = -b/2, y = h/2:
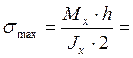 61*106 Па = 61 МПа.
61*106 Па = 61 МПа.
Минимальное напряжения достигаются в точке В (b/2,-h/2). В данном случае ( в силу отсутствия напряжения-сжатия)
![]() МПа.
МПа.
Эпюра нормальных напряжений прямолинейна. Её строим между двумя прямыми , проведенных параллельно нулевой линии.
Максимальные касательные напряжения от поперечных сил Qx , Qy определяем с помощью формулы Журавского:
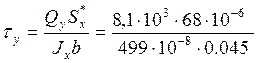 = 6.63*106 Па = 6.63
МПа
= 6.63*106 Па = 6.63
МПа
Эпюры ![]() показывают
изменение ка-
показывают
изменение ка-
сательных напряжений от изгиба вдоль
одноименной оси (рисунок 5).
Опасное сечение находится в состоянии
косого изгиба. Поэтому условие прочно-
сти для него будет
![]() МПа
МПа
В нашем случае
![]() МПа,
следовательно
МПа,
следовательно
условие прочности для первого
стержня выполняется.
Расчет на прочность стержня 2
Этот стержень работает на …Опасным является сечение 4, так как в нем действуют максимальный изгибающий и крутящий моменты (рисунок 6). Вычерчиваем это сечение в рабочем положении с действующими в нем силовыми факторами.
Qy = qa = 2.7 кН;
Qx = 3qa = 8.1 кН
N = 0
Mx = 0.5qa2 = 1 кН*м
My = 3qa2 = 5,5 кН*м
Mk = 3qa2 = 5,5 кН*м
Нормальные напряжения в опасном сечении определяются суммой напряжений от изгибающих моментов и продольной силы:
Геометрические характеристики рас-
сматриваемого сечения будут следу-
ющими ( d = h = 0.1 м):
![]() м2,
м2,
![]() м2,
м2,
![]() м3,
м3,
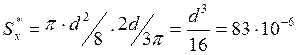 м3.
м3.
Нормальные напряжения в опасном сечении определяются суммой напряжений от изгибающих моментов и продольной силы:
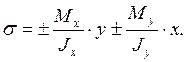
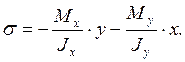
Уравнение нулевой линии:
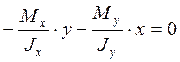 y = -
y = - 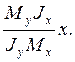
Нулевая линия проходит через центр тяжести сечения в первом и третьем квадратах (рисунок 5), с углом наклона к оси х:
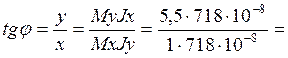 5,5 , φ=79,70.
5,5 , φ=79,70.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.