Определим координаты точек, наиболее удалённых от нулевой линии.
Точка А: xA = d*cosφ/2 = 0.11*0,179 /2 = 1*10-2 м;
yA = d*sinφ/2 = 0.11*0,984 /2 = 5,41*10-2 м.
Точка В: xВ = -xА = -1*10-2, yВ = -yA = -5.41*10-2 м.
Максимальные напряжения достигаются в точке А.
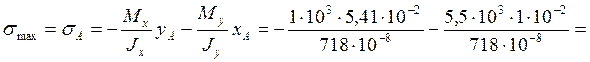 15,2*106 Па = 15,2 МПа.
15,2*106 Па = 15,2 МПа.
Минимальные напряжения достигаются в точке В.
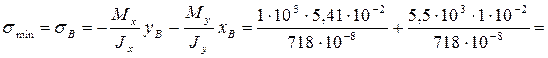 15,2*106
Па = 15,2 МПа.
15,2*106
Па = 15,2 МПа.
Максимальные касательные напряжения от поперечных сил Qx , Qy определяем с помощью формулы Журавского:
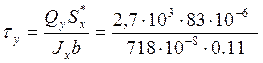 =
0,28*106 Па = 0,28
МПа.
=
0,28*106 Па = 0,28
МПа.
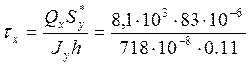 = 0.85*106 Па = 0,85 МПа
= 0.85*106 Па = 0,85 МПа
Наибольшие касательные напряжения от кручения достигаются в точках D и E:
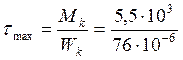 = 72*106 Па = 72
МПа,
= 72*106 Па = 72
МПа,
σэкв
= ![]() = 144,8 МПа
= 144,8 МПа
Следовательно, условие прочности для второго бруса выполняется.
Расчет на прочность стержня 3
Этот стержень работает на сжатие, кручение и на поперечный изгиб в двух плоскостях. Опасным является сечение 5, так как в нем действуют максимальный изгибающий и крутящий моменты. Вычерчиваем это сечение в рабочем положении с действующими в нем силовыми факторами (рисунок 8).
Qy = 0,5qa = 1,35 кН;
N = -3qa = -8,1 кН
Mx = 3qa2 = 5,5 кН*м
My = 3qa2 = 5,5 кН*м
Mk = 0,5qa2 = 1 кН*м
Геометрические характеристики рас-
сматриваемого сечения будут такими
же как у первого стержня:
|
Jx=bh3/12= |
499 |
*10-8 |
м4, |
|
|
Jy=hb3/12= |
84 |
*10-8 |
м4, |
|
|
S*x=bh/2*h/4=bh2/8= |
68 |
*10-8 |
м4, |
|
|
S*x=bh/2*b/4=hb2/8= |
28 |
*10-8 |
м4. |
|
F = 50 см2
Момент сопротивления при кручении прямоугольного стержня вычисляется по формуле
![]()
![]() определяем
интерполяцией с помощью таблицы 3,1
определяем
интерполяцией с помощью таблицы 3,1
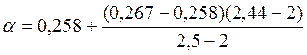 =
0,266
=
0,266
Wк = 0,266*0,11*0,0452 = 59*10-6 м3.
Аналогично определяется ![]()
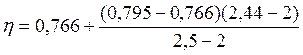 =
0,792
=
0,792
Нормальные напряжения в опасном сечении определяются суммой напряжений от изгибающих моментов и продольной силы:
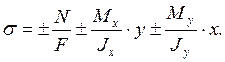
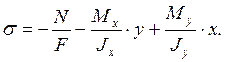
Уравнение нулевой линии:
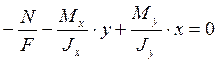
Нулевая линия не проходит через начало координат. Получим точки пересечения ее с координатными осями (рисунок 9):
1. Если х1 = 0, то 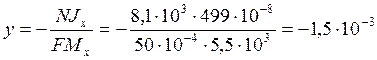 м;
м;
2. Если y2 = 0, то 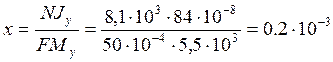 м.
м.
Максимальные напряжения достигаются в точке А(b/2;-h/2)
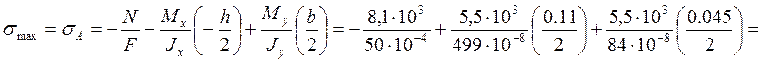
206,3*106 Па = 206,3 МПа.
Минимальные напряжения достигаются в точке В(-b/2;h/2).
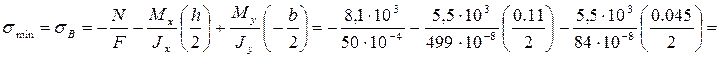
= 210 *106 Па = 210 МПа.
Максимальные касательные напряжения от поперечных сил Qx , Qy определяем с помощью формулы Журавского:
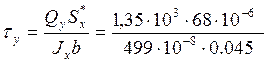 =
0,4*106 Па = 0,4 МПа
=
0,4*106 Па = 0,4 МПа
Наибольшие касательные напряжения от кручения достигаются в точках D и E:
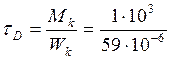 = 17*106 Па = 17
МПа,
= 17*106 Па = 17
МПа,
![]() = 0,792*17 = 14 МПа.
= 0,792*17 = 14 МПа.
Проверку прочности бруса проведём, сравнивая максимальное из напряжений в трёх точках с расчетным сопротивлением:
max(![]() )
)![]() МПа.
МПа.
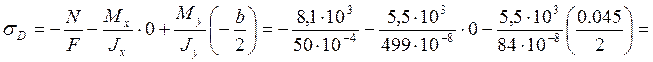 149
МПа
149
МПа
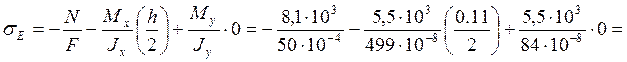 62
МПа
62
МПа
Эквивалентные напряжения в этих точках будут следующие:
σэквD = ![]() =
153 МПа
=
153 МПа
σэквE = ![]() =
68 МПа
=
68 МПа
Таким образом, условие прочности
по третьей теории для стержня
выполняются.
Задача 2.
Для расчета схемы стойки (рисунок10, а) требуется:
1) подобрать необходимый номер профиля проката заданного сечения стержня
(рисунок 10, б), приняв l = 5,6 м, Р = 400 кН, R = 210 Мпа, σт = 240 Мпа;
2) определить размер c из условия равноустойчивости сечения;
3) определить величину критической силы и коэффициент запаса на устойчивость по отношению к заданной нагрузке.
Так как в данном случае условие устойчивости содержит два неизвестных параметра – коэффициент уменьшения допускаемых напряжений и площадь поперечного сечения, то подбор размеров поперечного сечения проведём с помощью метода последовательных приближени.
На первом шаге коэффициент уменьшения допускаемых напряжений задаётся произвольно. Принимаем φ= 0,75. Затем из условия устойчивости через нагрузку и расчетное сопротивление получаем площадь всего сечения
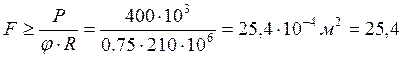 см2
см2
Для одного уголка
F1 = F/4 = 25,4/4 = 6,3см2
Согласно таблице сортамента
выбираем уголок 63![]() 63
63![]() 6
с площадью Fт = 7,28 см2. Так как
размер с неизвестен, то мы не можем определить растояние до оси x. Поэтому расчеты будем вести относительно оси у. Момент
инерции всего сечения относительно этой оси будет
6
с площадью Fт = 7,28 см2. Так как
размер с неизвестен, то мы не можем определить растояние до оси x. Поэтому расчеты будем вести относительно оси у. Момент
инерции всего сечения относительно этой оси будет
![]()
где JyT = 27,1 см4 – табличное значение момента инерции выбранного уголка
z0 = 1,64 см – характерный размер уголка
Тогда
![]() 4149
см4
4149
см4
Радиус инерции всего сечения
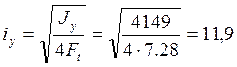 см
= 0,119
см
= 0,119
Коэффициенты приведения длины стержня … принимаем в соответствии со схемой закрепления концов стержня:
![]()
Гибкость относительно оси у
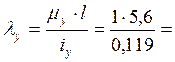 46,9.
46,9.
Соответствующий этой гибкости коэффициент уменьшения допускаемых напряжений … получим, интерполируя соседние значения в таблице 9.1. Так как
![]()
![]()
то
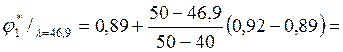 0,899
0,899
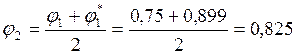
Разница между коэффициентами составила больше 5%, поэтому для второго шага принимаем φ= 0,825
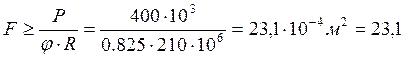 см2
см2
Для одного уголка
F1 = F/4 = 23,1/4 = 5,8см2
Согласно таблице сортамента
выбираем уголок 70![]() 70
70![]() 4,5
с площадью Fт = 6,20 см2. Так как
размер с неизвестен, то мы не можем определить растояние до оси x. Поэтому расчеты будем вести относительно оси у. Момент
инерции всего сечения относительно этой оси будет
4,5
с площадью Fт = 6,20 см2. Так как
размер с неизвестен, то мы не можем определить растояние до оси x. Поэтому расчеты будем вести относительно оси у. Момент
инерции всего сечения относительно этой оси будет
![]()
где JyT = 29,04 см4 – табличное значение момента инерции выбранного уголка
z0 = 1,88 см – характерный размер уголка
Тогда
![]() 3616 см4
3616 см4
Радиус инерции всего сечения
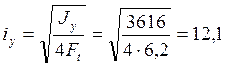 см
= 0,121
см
= 0,121
Коэффициенты приведения длины стержня … принимаем в соответствии со схемой закрепления концов стержня:
![]()
Гибкость относительно оси у
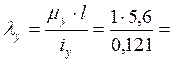 46,4.
46,4.
Соответствующий этой гибкости коэффициент уменьшения допускаемых напряжений … получим, интерполируя соседние значения в таблице 9.1. Так как
![]()
![]()
то
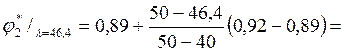 0,928
0,928
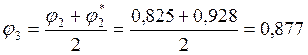
![]() 6%
6%
Разница между коэффициентами составила больше 5%, поэтому для второго шага принимаем φ= 0,877
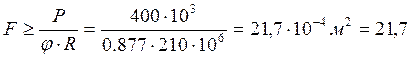 см2
см2
Для одного уголка
F1 = F/4 = 21,7/4 = 5,4см2
Согласно таблице сортамента
выбираем уголок 56![]() 56
56![]() 5
с площадью Fт = 5,41 см2. Так как
размер с неизвестен, то мы не можем определить растояние до оси x. Поэтому расчеты будем вести относительно оси у. Момент
инерции всего сечения относительно этой оси будет
5
с площадью Fт = 5,41 см2. Так как
размер с неизвестен, то мы не можем определить растояние до оси x. Поэтому расчеты будем вести относительно оси у. Момент
инерции всего сечения относительно этой оси будет
![]()
где JyT = 16 см4 – табличное значение момента инерции выбранного уголка
z0 = 1,57 см – характерный размер уголка
Тогда
![]() 2961 см4
2961 см4
Радиус инерции всего сечения
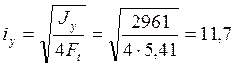 см
= 0,117
см
= 0,117
Коэффициенты приведения длины стержня … принимаем в соответствии со схемой закрепления концов стержня:
![]()
Гибкость относительно оси у
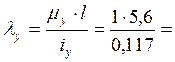 47,9.
47,9.
Соответствующий этой гибкости коэффициент уменьшения допускаемых напряжений … получим, интерполируя соседние значения в таблице 9.1. Так как
![]()
![]()
то
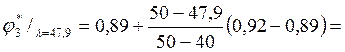 0,921
0,921
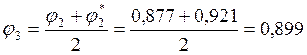
![]() 2,5%
2,5%
Окончательно принимаем уголок из последнего приближения. Табличные моменты инерции этого уголка
![]() см4,
см4,
Неизвестный размер сечения с
определяем из условия равноустойчивости сечения: ![]() .
Тогда
.
Тогда
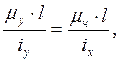
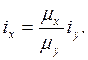
Радиусы инерции связаны с моментами инерции сечения соотношениями
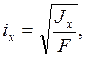
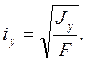
Подставляя их в предыдущее соотношение между радиусами инерции, получаем связь между моментами инерции:
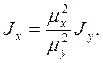
Используя выражения для моментов инерции относительно оси х
![]()
получим
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.