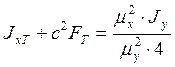
Отсюда с учетом того, что Jy = 4092 см4, следует размер с:
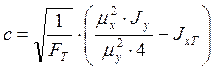 =
=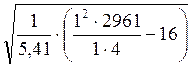 = 11,57 см.
= 11,57 см.
Величина критического напряжения в рассматриваемом случае вычисляется по формуле Ясинского, так как значение гибкости стержня λ=47,9 находится в интервале 40<λ <100:
![]() =
255 МПа.
=
255 МПа.
Критическая сила
![]() Н
= 553 кН.
Н
= 553 кН.
Коэффициент запаса на устойчивость
![]()
Задача 3.
Для фермы на (рисунке 11, а) проверить, достаточно ли сечения у стержней 1, 2, 3, если
Р =750 кН,
l = 3м,
R = 210Мпа.
Форма поперечного сечения показана на (рисунке 11, б) Считается, что стержни соединены шаровыми шарнирами, а составные сечения равноустойчивы.
Опорные реакции определяем из условия равенства нулю суммы моментов действующих сил:
Для определения усилий в стержнях 1 и 2 проведём сечение I-I, отбросив правую часть (рисунок 12, а)
Ra=0,375P
Rb=0,625P
Из условия равновесия , получим
![]() , получим
, получим 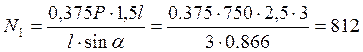 кН.
кН.
Проектируя силы на вертикальную ось, получим
![]()
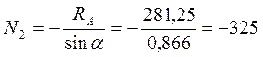 кН
кН
Проектируя силы на горизонтальную ось, получим
![]()
![]() кН
кН
Стержень 1. Стержень растянут, поэтому проверим выполнение условия прочности. Для этого вычисляем максимальное рабочее напряжения и сравним их с расчетным сопротивлением. Так как сечение состоит из двух … , то площадь
![]() см2.
см2.
Тогда
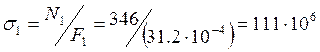 Па = 111 МПа < R = 210 МПа.
Па = 111 МПа < R = 210 МПа.
Условие прочности выполняется, следовательно, сечение достаточно.
Стержень 2. Стержень сжат, поэтому проверим выполнение условия устойчивости
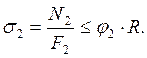
Сечение
стержня состоит из двух 90![]() 56
56![]() 8. Его площадь
8. Его площадь
F2 = 2*11.18 = 22.36 см2.
Стержни
скреплены шаровыми шарнирами, следовательно, коэффициент приведения длины ![]() . По условию задачи сечение
равноустойчиво, поэтому гибкость стержней в обоих направлениях одинакова
. По условию задачи сечение
равноустойчиво, поэтому гибкость стержней в обоих направлениях одинакова ![]() . Следовательно, и радиусы инерции
равны. Для расчета удобно взять ix, так как соответствующая ось совпадает с табличной осью
для данного уголка:
. Следовательно, и радиусы инерции
равны. Для расчета удобно взять ix, так как соответствующая ось совпадает с табличной осью
для данного уголка:
ix = ixT = 2.85 см
Вычисляем гибкость стержня:
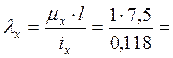 87,7
87,7
Коэффициент понижения допустимого напряжения ф2 определяем по таблице 9.1 в зависимости от полученной гибкости, используем метод интерполяции.
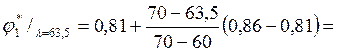 0,843
0,843
Допустимые напряжения для рассматриваемого стержня при расчетах на устойчивость будут следующие:
![]() 148 МПа.
148 МПа.
Рабочие напряжения
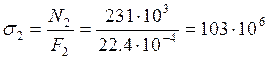 Па = 103 МПа.
Па = 103 МПа.
Так
как ![]() <
< ![]() МПа,
то условие прочности выполняется и сечение стержня 2 достаточно.
МПа,
то условие прочности выполняется и сечение стержня 2 достаточно.
Стерже6нь 3. Стержень сжат. Проверим выполнение условия устойчивости
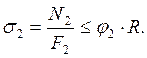
Для двутавра №18 площадь поперечного сечения F = … Гибкость стержня
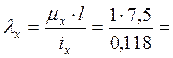 87,7
87,7
Коэффициент понижения допустимого напряжения ф3 определяем по таблице 9.1 в зависимости от полученной гибкости, используем метод интерполяции.
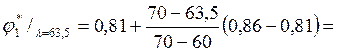 0,84
0,84
Допустимые напряжения для рассматриваемого стержня при расчетах на устойчивость будут следующие:
![]() 148 МПа.
148 МПа.
Рабочие напряжения
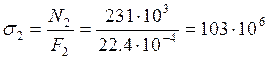 Па = 103 МПа.
Па = 103 МПа.
Так
как ![]() <
< ![]() МПа,
то условие прочности выполняется и сечение стержня 2 достаточно.
МПа,
то условие прочности выполняется и сечение стержня 2 достаточно.
Задача 4.
Груз весом Р падает на балку длиной l двутаврового сечения (№16) с высоты h. Рассмотреть два случая закрепления балки:
а) балка установлена на жёсткие неподвижные опоры (рисунок 13, а);
б) балка установлена на опоры одна из которых подрессорена пружиной, имеющей податливость Со (рисунок 13, б).
Р = 4,2 кН а = 0,6l
l = 2,6 м b = 0,4l
h = 0,12 м E = 2*105 МПа
Cо= 3 м/МН Jx = 873 см4
Wx = 109 см3
1.Реакции опор от статического воздействия груза Р определяем из уравнений моментов. Рассматривая точку В
![]()
Аналогично для точки А
![]() .
.
Эпюра изгибающих моментов
на каждом участке прямолиней-
на. Её наибольшее значение
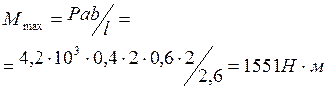
Максимальные статические
напряжения будут
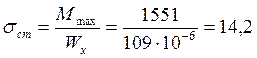 МПа
МПа
Дифференциальное уравнение упругой линии составим на последнем участке балки для произвольного сечения с координатой z:
![]()
После двукратного интегрирования получим
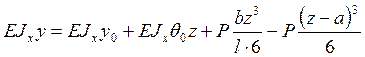 (1)
(1)
Здесь 0, yo – угол поворота и прогиб начального сечения балки. Они определяются из условий равенства нулю прогиба на опорах. Следовательно, на левой опоре y = yo = 0. На правой опоре при z = l
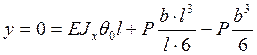
Отсюда
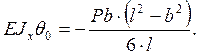
Статический прогиб wст находим как абсолютную величину прогиба y, подставив в формулу (1) координату z = a:
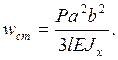
Подставляя данные задачи, вычисляем
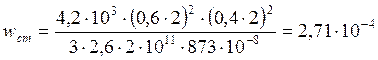 м.
м.
Динамический коэффициент определяем по следующей формуле:
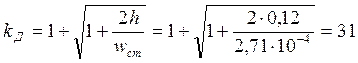
Наибольшее динамическое напряжение определяем используя следующее соотношение:
![]() МПа.
МПа.
Так как ![]() >R=210 МПа
, то условие прочности в данный момент не выполняется
>R=210 МПа
, то условие прочности в данный момент не выполняется
2.Рассмотрим случай, когда балка установлена на опоры, одна из которых подрессорена пружиной. Полный статический прогиб балки под грузом будет складываться из вычисленного ранее wст и дополнительного прогиба d, образовавшегося за счет сжатия пружины:
![]()
Для определения величины d воспользуемся подобием треугольников:
![]()
Отсюда ![]() , где
, где ![]() -
прогиб балки на левой опоре за счет сжатия пружины,
-
прогиб балки на левой опоре за счет сжатия пружины,
![]() м,
м,
![]() м.
м.
Теперь
![]() м,
м,
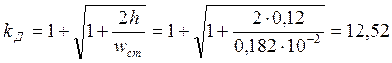 ,
,
![]() МПа.
МПа.
Так как ![]() <R=210 МПа
, то условие прочности в данный момент выполняется.Динамическое напряжение
здесь уменьшиться в
<R=210 МПа
, то условие прочности в данный момент выполняется.Динамическое напряжение
здесь уменьшиться в 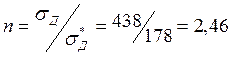 раза.
раза.
Стенд для исследования колебательных процессов имеет вибрационное устройство весом Р=9,5 кН, его вал вращается со скоростью n = 980 об/мин. Вследствие неуравновешенности вращающихся частей на двутавровую балку (№ 24, Jx = 3460 cм4; Wx = 289 см3) длиной l = 2,1 м действует также центробежная сила Рi = 0,7 кН. Модуль Юнга Е = 2*105 МПа (рисунок 14).
Статический прогиб балки от веса Р определяем по формуле
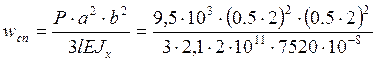 =
1*10-4 м.
=
1*10-4 м.
Частота свободных колебаний балки
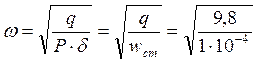 =
313 с-1
=
313 с-1
Частота внутренних колебаний φ определяется по круговой скорости вращения вала:
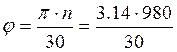 = 103 с-1.
= 103 с-1.
Динамический коэффициент вычисляется по следующей формуле
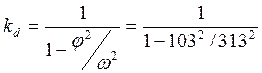 = 1,12 .
= 1,12 .
Постоянная составляющая часть напряжения от действующего веса Р
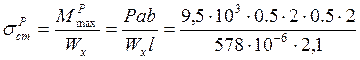 =
7,8*106 Па = 7,8 МПа.
=
7,8*106 Па = 7,8 МПа.
Максимальное динамическое составляющая часть напряжений от действия возмущающей силы Рi определяется как произведение статической составляющей от этой силы на динамический коэффициент:
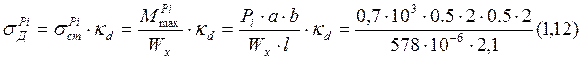 = 0,6*106 Па = 0,6МПа
= 0,6*106 Па = 0,6МПа
Так как центробежная сила в начальный момент времени равна нулю и действует периодически, то полное напряжение будет изменятся циклически по следующему закону:
![]()
Подставляя сюда вычисленные ранее значения напряжений, получаем
![]()
Цикл изменения напряжений несимметричный, его основные характеристики следующие:
σmax=8,5 МПа, σmin= 7,2 МПа, σm=( σmax+ σmin)/2 = 7,8МПа, σа=( σmax- σmin)/2 = 0,6 Мпа
Изображаем цикл графически (рисунок 15).
Система войдёт в резонанс, если совпадут частоты внутренних и свободных колебаний:
φ1 = ω. Резонансная скорость вращения вала будет
![]() = 2987 об/мин
= 2987 об/мин
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.