Проектирование выправки существующей кривой. Проектирование реконструкции продольного профиля. Проектирование плана второго пути. Проектирование поперечных профилей земляного полотна

Содержание

1 Проектирование выправки существующей кривой

Проектирование выправки “сбитых” или расстроенных железнодорожных кривых включает в себя:

ü  определение радиуса такой правильной кривой, при котором обеспечивается получение рациональных по величине и направлению рихтовок (сдвигов, сдвижек);

ü  установление остальных элементов правильной кривой – угла поворота, тангенса и длины круговой кривой, длины переходной кривой;

ü  определение положения кривой в пикетаже;

ü  подсчёт в каждой точке деления кривой рихтовок, которые надо осуществить для приведения существующей кривой в правильное геометрическое очертание.

Решить указанные задачи можно разными методами. Большая группа методов приспособлена к особенностям, возникающими при текущем содержании пути (методы П.Г.Козийчуга, А.Т.Крагеля, М.Д.Поликарпова, М.А.Макурова и др.).

При проектировании реконструкции плана линии, когда необходимо бо­лее точно установить параметры проектируемых кривых, применяются спе­циальные методы. Наибольшее распространение в проектных организациях получил метод с использованием угловых диаграмм кривых. Этот метод разработан канд. техн. наук И.3.Гоникбергом.

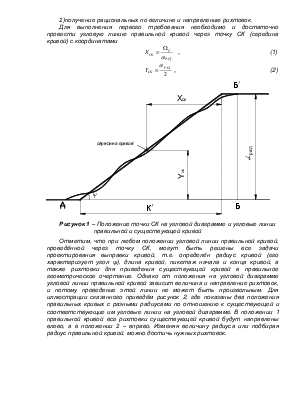
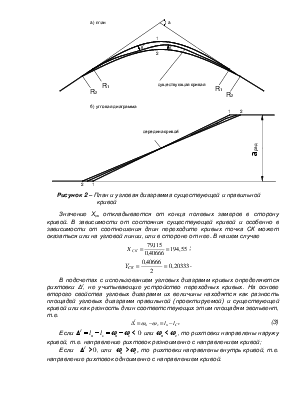
1.1 Построение угловой диаграммы существующей кривой

Угловая диаграмма кривой – это зависимость угла поворота от длины кривой: . Угловая линия правильной круговой кривой на угловой диаграмме – прямая с угловым коэффициентом

                                         ,

так как кривая на всём протяжении имеет постоянную кривизну. Кривизна же расстроенной кривой в различной её точках неодинакова, что отражается на очертании угловой линии.

По результатам полевой съёмки получены углы α₁, α₂, …α₆ между основными хордами длиной, кратной 20 м, а также стрелы f на «двадцатках в пределах каждой хорды (из задания). Все расчёты производим в ведомости (см. приложение). Левая часть ведомости содержит материалы обработки съёмки существующей кривой и определения площади её угловой диаграммы, а правая часть – материалы проектирования выправки кривой: подбор радиуса, длины переходной кривой и определение сдвигов.

Угловая диаграмма кривой строится на миллиметровой бумаге в масштабах:

горизонтальный (масштаб длин) - 1 : 1000 или 1 см = 10 м;

вертикальный (масштаб углов) - 1 см = 0,02 рад.

На оси абсцисс в масштабе длины отмечаются все пикеты и плюсы ("двадцатки") от начала до конца съемки кривой. В последней точке откладывается по вертикали величина угла поворота кривой α_рад и через полученную точку проводится горизонтальная линия 80 - 100 м в сторону кривой.

Для наколки угловой линии существующей кривой используются данные графы 7 ведомости, где содержатся двадцатикратные значения углов. В целях исключения необходимости опре­деления на каждой "двадцатке" действительных значений φ на оси орди­нат вводится вспомогательный масштаб углов 1 см = 0,40 рад. (По сравнению с основным масштабом он в 20 раз мельче). В этом масштабе и откладываются на угловой диаграмме значения углов 20φ_рад из графы 7. По шкале основного масштаба (1 см = 0,02 рад) эти углы будут равны действительному значению 20φ_рад.

Углы φ соответствуют касательным к кривой в середине "двадцаток" . Поэтому и значения 20φ_рад = ω_э надо откладывать в середине "двадцаток". Наколотые точки соединяются прямыми линиями. Полученная ломаная линия вместе с продолжением ее до точек, соответствующих началу и концу съемки (точки А и Б), является угловой линией существующей кривой.

В расчетах и построениях, связанных с угловыми диаграммами, следует иметь в виду, что углы в радианах - величины безразмерные, а площади угловой диаграммы ω_э и ω_с  имеют линейную размерность - м. Однако на шкале вспомогательного вертикального масштаба, с использованием кото­рого на угловой диаграмме откладываются значения ω_э = 20φ_рад, эту размерность проставлять не следует так как сама эта шкала, заменяя деление ώ_э на 20 м, переводит линейные  величины (ω_э) в безразмерные (20φ_рад ).

В процессе подсчёта ведомости для контроля расчётов используются три проверки:

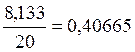1.  Последнее значение , разделённое на 20, должно быть равно . В данном случае . Расхождение полученной величины с  составляет , что находится в пределах допуска.

2.  На каждой основной хорде сумма положительных  должна быть равна сумме отрицательных , а абсолютное значение каждой из этих сумм должно быть равно наибольшей стреле, т.е. . Например, на второй основной хорде

                                            ;

      ;

         .

3.  В точках, соответствующих теодолитным стоянкам в строках над линиями подчёркивания, величина  должна быть равна сумме величин , записанных в графе 4 для всех предыдущих теодолитных стоянок, т.е. .

В данном случае значения  равны:

на  ПК 251 →3,528;

 ПК 252 →3,528+18,180=21,708;

ПК 253  →3,528+18,180+33,305;

ПК 254  →3,528+18,180+33,305+24,102=79,115 (Ω_с).