Використання дисперсійного аналізу для перевірки адекватності регресійної моделі. Побудова класичної множинної моделі лінійної регресії

Модуль 2. Економетричні методи і моделі в аналізі  соціально-економічних систем

Лабораторна робота №6

Використання дисперсійного аналізу для перевірки адекватності регресійної моделі

6.1. Мета роботи – ознайомлення з особливостями побудови математичної моделі парної регресії, що передбачає вибір найкращого рівняння за допомогою обчислення помилки апроксимації.

6.2. Змістовна постановка задачі та її математична модель

Парна регресія – рівняння зв’язку двох змінних  та , де  – залежна змінна (результативна ознака);  – незалежна, пояснювальна змінна (ознака-фактор).

Рівняння лінійної парної регресії має вид:  .

Нелінійні регресії розподіляються на два класи: нелінійні відносно пояснюючих змінних (поліноми різних степенів, рівнобічна гіпербола) та нелінійні за параметрами (степенева, показникові, експоненціальна та ін.). Відзначимо, що деякі нелінійні моделі можна перетворити до виду лінійної.

Побудова рівняння регресії здійснюється в два етапи:

специфікація моделі (визначення виду аналітичної залежності ();

оцінка параметрів обраної моделі.

Використовуються три основні методи вибору аналітичної залежності: графічний (на основі аналізу поля кореляцій); аналітичний  (на основі теорії вивчення взаємозв’язку) та експериментальний  шляхом порівняння величини залишкової дисперсії або середньої помилки апроксимації.

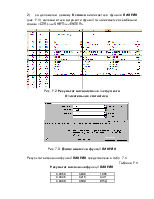
Для оцінки параметрів рівняння лінійної регресії використовують метод найменших квадратів (МНК). МНК дозволяє одержати такі оцінки параметрів, при яких сума квадратів відхилень фактичних значень результативної ознаки від теоретичних є мінімальною.

Умова мінімізації вказаної функції веде до розв’язання системи рівнянь, на основі якої отримано формули коефіцієнтів регресії:   

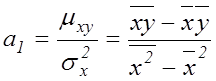          ,       ,                          (6.1)

де 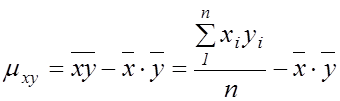      – коефіцієнт коваріації,

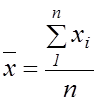 – середнє значення пояснювальної змінної ,

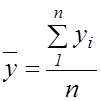 – середнє значення результативної ознаки ,

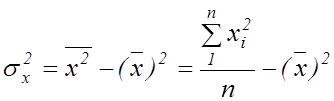 – дисперсія .

Для оцінки тісноти зв'язку використовується лінійний коефіцієнт парної кореляції для лінійної регесії:

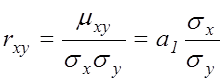                                                                                 (6.2)

та індекс кореляції для нелінійної регресії:

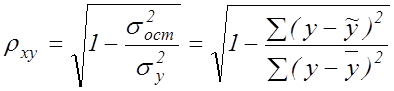                              ,                      (6.3)

де 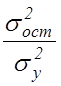 – доля остаточної дисперсії в загальній.

Для визначення якості обраної моделі обчислюється середня помилка апроксимації, як середнє арифметичне відносних відхилень за кожним спостереженням:

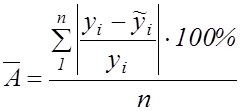                             .                                      (6.4)

          Припустима межа середньої помилки апроксимації – не більш ніж 8-10%.

Щоб визначити на скільки відсотків в середньому за сукупністю зміниться результативна ознака від свого середнього значення за умовою зміни пояснювального фактора на 1% від свого середнього значення обчислюється середній коефіцієнт еластичності:

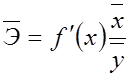                                       .                                              (6.5)

Також, щоб оцінити якість лінійної моделі та визначити, на скільки відсотків дисперсія результативної ознаки пояснюється мінливістю обчислюється коефіцієнт детермінації:

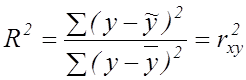                             .                                     (6.6)

          Коефіцієнт детермінації використовується в -тесті, що перевіряє  гіпотезу про статистичну незначущість рівняння та показника тісноти зв’язку. Для цього виконується порівняння табличного значення  (додаток А) для відповідного рівня значущості та фактичного значення

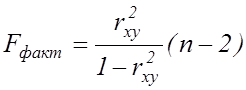                                       .                                     (6.7)

          Якщо , то підтверджується статистична значущість та надійність рівняння регресії. Якщо , то визнається статистична незначущість рівняння.

          Для оцінки статистичної значущості коефіцієнтів лінійної регресії та лінійного коефіцієнта парної кореляції обчислюється -критерій Стьюдента та обчислюються довірчі інтервали кожного з показників.

          Відповідно -критерію висувається  гіпотеза про випадкову природу показників та їх незначну різницю від нуля. Обчислюються фактичні значення критерія для коефіцієнтів регресії та коефіцієнта кореляції: 

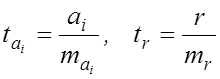                                       ,                                         (6.8)

де      – середні помилки параметрів лінійної регресії,

 – середня помилка коефіцієнта кореляції, які визначаються за формулами:

;

;

.

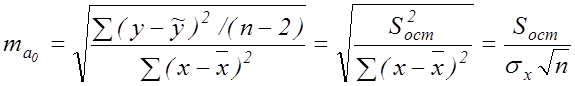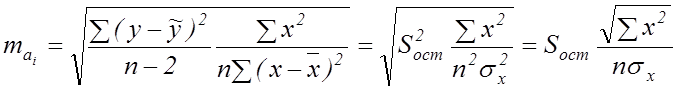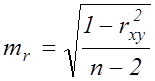Порівнюючи фактичне та табличне значення -статистики    (додаток Б) ми приймаємо або відхиляємо  гіпотезу про випадкову природу параметрів моделі та коефіцієнту кореляції. Якщо, , то гіпотеза відкидається, підтверджується статистична значущість коефіцієнтів моделі і кореляції. Якщо, , то визнається статистична незначущість коефіцієнтів та випадковість їх формування.

Побудову довірчих інтервалів здійснюють для оцінки відхилень емпіричних значень параметрів моделі від точних. Для обчислень довірчих інтервалів визначається гранична помилка для кожного параметра:    ,

Величина  це табличне значення -критерія Стьюдента під впливом випадкових факторів  за  ступенями свободи та заданому рівні значущості.

Формули для обчислень довірчих інтервалів мають наступний вигляд:

                    , .                                  (6.9) 

6.3. Завдання

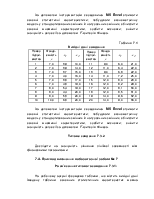
У таблиці представлені значення ціни та товар (грн) і обсяг пропозиції (попиту), (тис.грн).

За допомогою функцій та надбудов середовища MSExcel побудувати лінійну, степеневу та показникову моделі, обчислити основні характеристики, зробити висновки щодо специфікації моделі.

6.4. Приклад виконання лабораторної роботи № 6

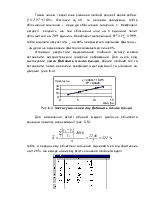
Для вибору виду рівняння моделі парної регресії проілюструємо графічно залежність вихідних даних за допомогою вбудованого пакету Мастер диаграмм (рис. 6.1).

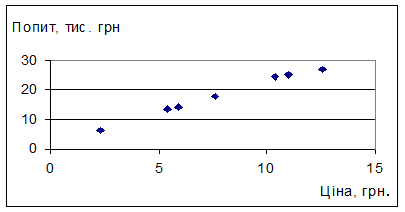Рис. 6.1. Графічна ілюстрація залежності вихідних даних

Графічне зображення надає можливість припустити про лінійний зв’язок: . Параметри означеної лінійної моделі можна обчислити за формулами (6.1) й за допомогою вбудованої функції ЛИНЕЙН().

      Для цього необхідно виконати наступний алгоритм дій:

1.  На робочому аркуші формується таблиця, що містить вихідні дані.

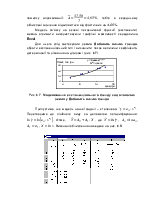
2. Виділяється блок (5 стрічок х 2 стовпчики) з метою визначення  результатів регресійної статистики.

          3. За допомогою режиму Вставка викликається функція ЛИНЕЙН() (рис. 6.2), заповнюються аргументи функції та натискається комбінацію клавіш <CTRL>+<SHIFT>+<ENTER>.

Рис. 6.2. Діалогове вікно функції ЛИНЕЙН()

Синтаксис функції ЛИНЕЙН():

Изв_знач_y — множина значень залежної змінної   (результативної ознаки). Якщо масив изв_знач_y має один стовпчик, то кожен стовпчик масиву изв_знач_x інтерпретується як окрема змінна. Якщо масив изв_знач_y має одну строку, то кожна строка масиву изв_знач_x інтерпретується як окрема змінна.