Використання дисперсійного аналізу для перевірки адекватності регресійної моделі. Побудова класичної множинної моделі лінійної регресії, страница 6

За допомогою інструментарію середовища MSExcel отримати основні статистичні характеристики; побудувати економетричну модель у стандартизованих змінних й натуральних змінних; обчислити основні множинні характеристики, зробити висновки; оцінити значущість регресії за допомогою F-критерія Фішера.

Типове завдання 7.3.2

Дослідити на значущість рівняння лінійної залежності між фінансовими показниками.

7.4. Приклад виконання лабораторної роботи № 7

Розв’язання типового завдання 7.3.1:

На робочому аркуші формуємо таблицю, що містить вихідні дані Зведену таблицю основних статистичних характеристик можна отримати за допомогою інструмента Описательная статистика в розділі Сервис/ Анализ данных.

На рис. 7.1 представлено діалогове вікно надбудови Описательная статистика.

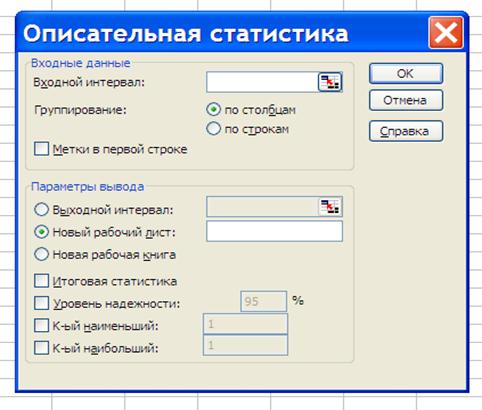
Рис. 7.1. Діалогове вікно надбудови Описательная статистика

Основні параметри вихідних даних надбудови Описательная статистика:

Входной інтервал – діапазон, який містить вихідні дані аналізу;

Группирование – по столбцам або по строкам – метод групування вихідних даних;

Метки – опція, яка визначає, чи містить перша стрічка назву стовпців чи ні;

Выходной интервал – місце розташування звіту.

Додатковою інформацією, що надається, є «Итоговая статистика», «Уровень надежности», «К-ый наименьший», «К-ый наибольший».

Результати обчислення відповідних показників для кожної ознаки представлено на рис. 7.2.

Параметри лінійної множиної моделі обчислюємо за допомогою вбудованої функції ЛИНЕЙН.

          Для цього необхідно виконати наступний алгоритм дій:

1)  виділяється блок (5 стрічок х 3 стовпчики) з метою визначення  результатів регресійної статистики;

2)  за допомогою режиму Вставка викликається функція ЛИНЕЙН (рис. 7.3), заповнюються аргументи функції та натискається комбінацію клавіш <CTRL>+<SHIFT>+<ENTER>.

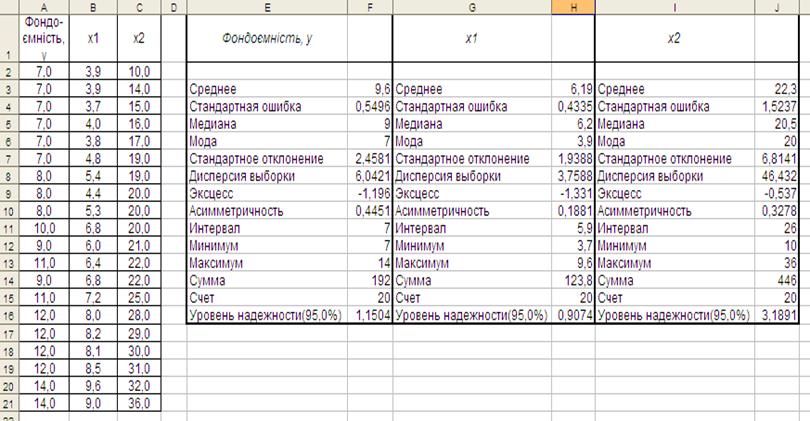Рис. 7.2. Результат використання інструмента

Описательная статистика

         

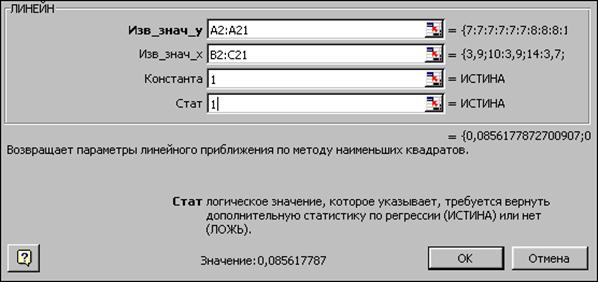Рис. 7.3. Діалогове вікно функції ЛИНЕЙН

Результат виконання функції ЛИНЕЙН представлено в табл. 7.1.

Таблиця 7.1

Результат виконання функції ЛИНЕЙН

Таким чином, теоретичне рівняння лінійної множиної регресії в натуральних змінних являє собою:

.

Для побудови моделі в стандартизованих змінних знайдемо значення за формулою (7.3):

, .

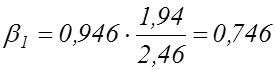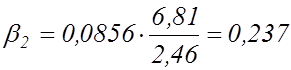Отже, модель в стандартизованих змінних має вигляд:

.

Завдяки тому, що , можна стверджувати, що витрати , які пов'язані з усуненням всіх видів простою, сильніше впливають на фондоємність  і фактор  є більш інформативним.

Коефіцієнт детермінації , тобто варіація результата на 95% пояснюється варіацією обраних факторів, на долю не врахованих факторів залишається 5%.

Знайдемо часткові коефіцієнти еластичності за формулою (7.4):

,   .

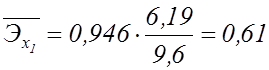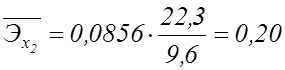Таким чином, можна зробити висновок, що зі збільшенням середньої величини витрат виробництва, пов'язаних з усуненням всіх видів простою (), на 1% середнє значення фондоємності (у) збільшиться на 0,61%; зі збільшенням середньої величини витрат виробництва, пов'язаних з модернізацією встаткування й удосконалюванням техніки й технології виробництва (), на 1% середнє значення фондоємності () збільшиться на 0,20%.

Використовуючи інструмент аналіза даних Корреляция, який знаходиться у розділі Сервис/Анализ данных, можна отримати матрицю парних коефіцієнтів кореляції змінних (Рис. 7.4).

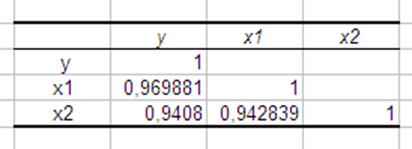
Рис. 7.4. Матриця коефіцієнтів парної кореляції

          Значення коефіцієнтів парної кореляції вказують на досить тісний зв’язок фондоємності (у) як з витратами виробництва, пов'язаними з усуненням всіх видів простою () так і з витратами виробництва, пов'язаними з модернізацією встаткування й удосконалюванням техніки й технології виробництва (). У той же час спостерігається досить тісний міжфакторний зв’язок.

          Коефіцієнти часткової кореляції дають можливість отримати більш точну характеристику тісноти зв’язку між ознаками за рахунок виключення парної залежності від взаємодії заданої пари ознак з іншими ознаками, які представлено в моделі.

          Для обчислення коефіцієнтів часткової кореляції скористаємось формулою (7.6) відповідно якої необхідно обчислити величини , , . Величину   можна взяти з табл. 7.1 (), а величини та  обчислити, використовуючи відповідні коефіцієнти лінійної кореляції і (рис. 7.4) – ; .

          Отже, отримуємо часткові коефіцієнти кореляції:

;     .

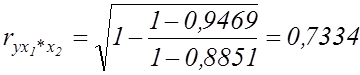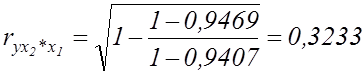          Оцінимо значущість часткових коефіцієнтів кореляції. Обчислимо фактичні значення часткового критерія Фішера за формулою (7.10):

;

.

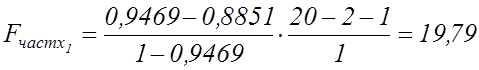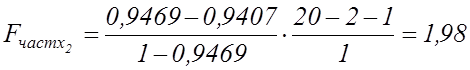Для визначення табличних значень  F-критерія Фишера доцільно використати вбудовану функцію Excel «FРАСПОБР» (рис. 7.5) з параметрами ,  та  або .

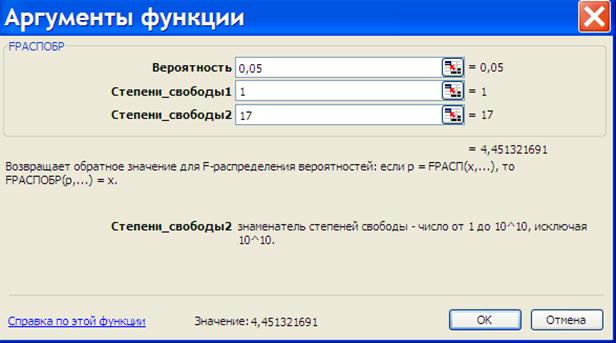
Рис. 7.5. Вікно параметрів функції FРАСПОБР

          Як результат отримуємо:

, .

          Оскільки фактичне значення  перевищує табличні значення, то це свідчить про значущість часткового коефіцієнта кореляції  та інформативність фактора . У той же час фактичне значення  менш ніж табличні значення, що вказує на незначущість часткового коефіцієнта кореляції  й не інформативність фактора .

          Оцінимо значущість рівняння регресії за допомогою F-критерія Фішера. Фактичне значення загального F-критерія: . Визначимо табличні значення F-критерія Фишера з параметрами  та  при рівні значущості  за допомогою «FРАСПОБР»:  .           Оскільки фактичне значення F-критерія Фішера перевищує табличні значення, можна із упевненістю 95% стверджувати, що рівняння регресії є значущим.

  Аналогічні результати можна отримати за допомогою вбудованого пакету Анализ данных. Для цього необхідно в меню Сервис обрати відповідний пункт і на екрані з’явиться вікно вибору методу аналізу     (рис. 7.6).

Рис. 7.6. Вікно вибору методу аналізу

          Обираємо пункт Регрессия і натискуємо кнопку ОК, з’явиться вікно, в якому необхідно задати параметри для проведення регресійного анализу   (рис. 7.7).