Тісноту сумісного впливу факторів на результат можна оцінити за допомогою коефіцієнта множинної кореляції:
або
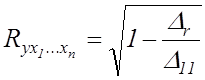, (7.5)
де 
– визначник матриці парних
коефіцієнтів кореляції; 
–
визначник матриці міжфакторної кореляції.
При проведенні багатофакторного аналізу обчислюються часткові коефіцієнти кореляції, які вимірюють вплив на результативну ознаку окремого фактора при незмінному рівні інших факторів:
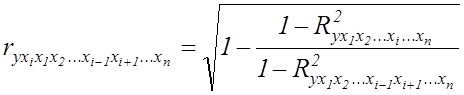(7.6)
або за рекурентною формулою:
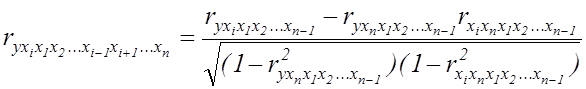. (7.7)
Якість
побудованої моделі в цілому можна оцінити за допомогою коефіцієнта (індекса)
детермінації: 
. Скоригований індекс
множинної детермінації містить поправку на кількість ступенів свободи й обчислюється за
формулою:
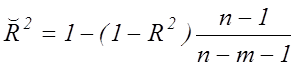. (7.8)
Значущість
рівняння множинної регресії в цілому оцінюється за допомогою 
-критерія
Фішера, фактичне значення якого одержуємо за
формулою:
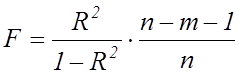, (7.9)
де 
– кількість спостережень; 
– кількість
факторів; 
– коефіцієнт (індекс) детермінації.
Доцільність присутності кожного з факторів у множинній моделі встановлюється за допомогою часткових F-критеріїв Фішера, які обчислюються для кожного фактора за формулою:
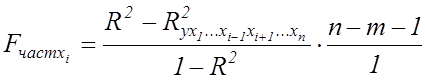. (7.10)
Оцінка
значущості коефіцієнтів регресії на основі 
-критерія Стьюдента приводить до
обчислення статистики:
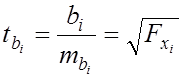, (7.11)
де 
- середня квадратична помилка
коефіцієнта регресії:
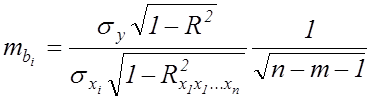. (7.12)
Поняття значущості пов'язано з тим, що коефіцієнти регресії обчислюються за даними вибірки і можуть відрізняться від аналогічних коефіцієнтів, які отримані за даними іншої вибірки. Тобто коефіцієнти регресії мають певну дисперсію навколо генеральної середньої. Якщо дисперсія коефіцієнтів регресії достатньо велика, то рівняння регресії не відображає достатньою мірою існуючі взаємодії факторів у генеральній сукупності. В цьому разі регресійна модель є у певній мірі випадковою і вважається як не значуща.
Слід зазначити, що знаходження дисперсії коефіцієнтів регресії на практиці є дуже складним і дорого коштує. Тому дисперсії визначають теоретично. Але існує й інший шлях, який дозволяє оцінити значущість моделі на основі тільки однієї вибірки.
Для того, щоб перевірити модель на значущість на основі тільки однієї моделі використовується дисперсійний аналіз.
При цьому обчислюється статистика Фішера:
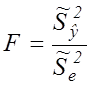(7.13)
де
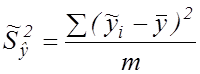– скорегована дисперсія обчислених значень,
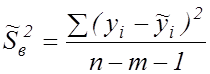– скорегована дисперсія залишкової похибки,
– кількість спостережень,
– кількість незалежних змінних
– середнє значення величин результативної ознаки,
– фактичні значення результативної ознаки,
– теоретичні значення результативної ознаки.
Якщо фактичне значення критерія Фішера (7.13)
перевищує табличне критичне значення 
,
де – обсяг вибірки,
– число
регресорів, 
– рівень значущості,
то -факторна лінійна модель значуща на
рівні . В протилежному випадку є підстави вважати, що сукупний
вплив пояснюючих змінних несуттєвий і загальна якість моделі низька.
На практиці замість перевірки гіпотези про статистичну
значущість моделі перевіряють гіпотезу про статистичну значущість коефіцієнта
детермінації 
.
Для перевірки означеної гіпотези використовується
наступна -статистика:
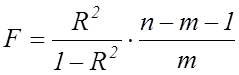, (7.14)
яка має розподіл Фішера.
Якщо фактичне значення критерія Фішера (7.14)
перевищує табличне критичне значення ,
то приймається гіпотеза про
статистичну значущість коефіцієнта детермінації. В протилежному випадку
гіпотеза про статистичну значущість коефіцієнта детермінації відхиляється.
Регресійна модель будується за даними
вибірки із статистичного ансамблю. Припустимо, що цей ансамбль складається із
числових значень економічних показників групи однорідних у певному сенсі
підприємств. Припустимо далі, що кількість показників дорівнює ,
а кількість підприємств дорівнює .
Тоді кількість факторів регресійної моделі дорівнює , а обсяг вибірки –
.
Якщо
регресійна модель, яка побудована за
даними підприємств,
значуща, то економічні результати, яки отримані за
допомогою цієї моделі можуть бути застосовані до інших підприємств даного
класу, незважаючи на те, що ми не аналізуємо їх балансових показників.
7.3. Завдання
Типове завдання 7.3.1
Проведено дослідження залежності фондоємності (грн/тис.грн) від х1 - витрат виробництва, що пов'язані з усуненням всіх видів простою (тис. грн.) та х2 - витрат виробництва, що пов'язані з модернізацією встаткування й удосконалюванням техніки й технології виробництва (тис. грн.) по 20-ти підприємствах.
У табл. 7.1 представлені вихідні дані.
За допомогою інструментарію середовища MSExcel отримати основні статистичні характеристики; побудувати економетричну модель у стандартизованих змінних й натуральних змінних; обчислити основні множинні характеристики, зробити висновки; оцінити значущість регресії за допомогою F-критерія Фішера.
Таблиця 7.1
Вихідні дані завдання
|
Номер підпри-ємства |
Фондо-ємність
|
|
|
Номер підпри-ємства |
Фондо-ємність
|
|
|
|
1 |
7,0 |
3,9 |
10,0 |
11 |
9,0 |
6,0 |
21,0 |
|
2 |
7,0 |
3,9 |
14,0 |
12 |
11,0 |
6,4 |
22,0 |
|
3 |
7,0 |
3,7 |
15,0 |
13 |
9,0 |
6,8 |
22,0 |
|
4 |
7,0 |
4,0 |
16,0 |
14 |
11,0 |
7,2 |
25,0 |
|
5 |
7,0 |
3,8 |
17,0 |
15 |
12,0 |
8,0 |
28,0 |
|
6 |
7,0 |
4,8 |
19,0 |
16 |
12,0 |
8,2 |
29,0 |
|
7 |
8,0 |
5,4 |
19,0 |
17 |
12,0 |
8,1 |
30,0 |
|
8 |
8,0 |
4,4 |
20,0 |
18 |
12,0 |
8,5 |
31,0 |
|
9 |
8,0 |
5,3 |
20,0 |
19 |
14,0 |
9,6 |
32,0 |
|
10 |
10,0 |
6,8 |
20,0 |
20 |
14,0 |
9,0 |
36,0 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
