Використання дисперсійного аналізу для перевірки адекватності регресійної моделі. Побудова класичної множинної моделі лінійної регресії, страница 4

16		17		18		19		20
Y	X	Y	X	Y	X	Y	X	Y	X
102,5	212,65	610,6	205,39	802,1	26,24	87,1	125,38	80,8	428,35
106,1	212,64	410,3	206,42	602,3	27,48	67,5	125,83	70,8	429,14
108,0	212,49	510,2	206,23	602,2	27,24	67,3	125,74	90,3	430,53
108,0	211,52	710,4	205,40	502,6	26,55	67,5	126,65	90,4	444,22
106,4	213,24	510,8	206,96	602,2	29,4	77,5	130,47	90,9	437,44
109,1	211,81	610,4	206,54	602,5	26,18	77,4	128,93	100,1	435,18
106,2	211,86	510,7	205,69	602,6	25,18	77,5	129,18	80,8	431,55
106,0	201,97	610,9	207,84	502,5	25,71	97,8	130,56	80,1	432,16
105,9	212,50	610,6	207,09	602,0	27,16	97,0	130,18	101,6	435,45
106,8	213,32	810,0	209,19	602,5	25,82	87,5	132,17	100,4	441,69
106,0	214,13	810,7	206,74	602,8	27,17	97,6	130,96	100,1	439,11
106,6	212,25	810,0	206,84	602,0	25,61	77,6	128,33	90,0	432,15

21		22		23		24		25
Y	X	Y	X	Y	X	Y	X	Y	X
206	12	35	215,39	45	206,24	50	25,38	60	218,35
208	22,64	36	216,42	46	207,48	52	25,83	66	219,14
205	22,49	39	216,23	46	207,24	51	25,74	65	310,53
208	21,52	40	215,40	49	206,55	63	26,65	70	314,22
300	23,24	35	216,96	40	209,4	60	30,47	74	317,44
302	21,81	30	216,54	42	206,18	62	28,93	72	315,18
305	21,86	35	215,69	40	205,18	65	29,18	70	311,55
300	20,97	40	217,84	41	205,71	68	30,56	75	312,16
402	22,50	42	217,09	42	207,16	62	30,18	72	315,45
405	23,32	45	219,19	45	205,82	65	32,17	76	411,69
500	24,13	43	216,74	50	207,17	60	30,96	70	319,11
305	22,25	39	216,84	43	205,61	55	28,33	65	312,15

     6.6. Контрольні запитання

1.  Моделі, що відносяться до категорії економетричних.

2.  Означення залежних (ендогенних) та незалежних (екзогенних) факторів.

3.  Задачі регресійного аналізу та їх відмінність від задач кореляційного аналізу.

4.  Етапи побудови економетричних моделей.

5.  Поняття про специфікацію економетричної моделі.

6.  Помилки специфікації та їх вплив на оцінки параметрів моделі.

7.  Умови, за якими можливо використання метода найменших квадратів.

8.  Властивості статистичних оцінок параметрів економетричної моделі, які отримані за методом МНК.

Лабораторна робота №7

Побудова класичної множинної моделі лінійної регресії

7.1. Мета роботи – ознайомлення з особливостями побудови математичної моделі лінійної множиної регресії.

7.2. Змістовна постановка задачі та її математична модель Множинна регресія – рівняння зв’язку декілька змінних:

                                                                                   (7.1)

          Множинна регресія використовується в ситуаціях, коли з множини факторів, які впливають на результативну ознаку, неможливо виділити один домінуючий фактор і необхідно враховувати вплив декількох факторів.

          Відбір факторів здійснюється на основі теоретично-економічного аналізу сутності проблеми.

Для побудови рівняння множинної регресії поширеною є лінійна функція: , оцінка параметрів якої здійснюється за методом найменьших квадратів (МНК). Параметри при змінних характеризують середні зміни результата у зв’язку зі змінами відповідного фактора за умовою незмінного значення інших факторів, яке закріплено на середньому рівні.

Інший вид рівняння множинної регресії - рівняння в стандартизованих змінних:

                              ,                                   (7.2)

де 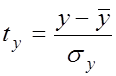,  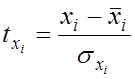– стандартизовані змінні, для яких , .

          За величиною -коефіцієнтів можна робити висновок про силу впливу факторів на результативну ознаку. Тобто за допомогою -коефіцієнтів можна ранжувати фактори за силою їх дії на результат.

          Зв’язок коефіцієнтів множинної регресії із стандартизованими коефіцієнтами можна описати співвідношенням:

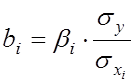                                                           ,                                    (7.3)

параметр .           

Середні коефіцієнти еластичності для лінійної множиної регресії обчислюються за формулою: 

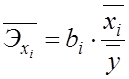                                       .                                                        (7.4)