




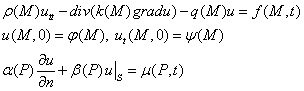
Определение. Классическим решением начально-краевой задачи называется функция непрерывная вместе с первыми производными в замкнутом цилиндре, имеющая непрерывные производные второго порядка в открытом цилиндре, удовлетворяющая уравнению, начальным и граничным условиям.
Доказательство.
Пусть ![]() -два
различных классических решения
-два
различных классических решения
В силу линейности функция ![]() является
решением следующей однородной начально-краевой задачи
является
решением следующей однородной начально-краевой задачи
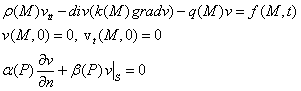
Построим интеграл
![]()
Покажем, что интеграл не меняется во времени
![]()
Воспользуемся первой формулой Грина
![]()
и подставим в предыдущее соотношение
![]()
Для первой и для второй
задачи ![]()
![]()
![]() из
начальных условий
из
начальных условий
![]()
Для третьей ![]()
Отсюда
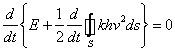
![]()
из
начальных условий ![]()
Итак,
для всех случаев ![]() и учитывая начальные условия
и учитывая начальные условия ![]()
Формальное построение решения
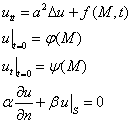
![]()
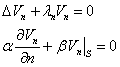
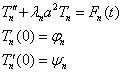
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.