Санкт-Петербургский государственный политехнический университет
Инженерно-строительный факультет
Кафедра гидравлики
Задание № 4 по курсу гидравлики
«Расчет канала трапецеидального поперечного сечения»
Выполнил студент гр. 3013/2: Кулакова М.Н.
Проверил: Локтионова Е.А.
Санкт-Петербург
2012г
Оглавление
1. Расчет канала на равномерное движение 2
1. 1. Определение глубины равномерного движения ho1 и ширины канала по дну b на подводящем участке канала при β=(βг.н.)пред.. 2
2. 1. Определение глубины равномерного движения на отводящем участке канала ho2 , полагая ширину канала b, равной найденной в п.1. 7
3. Определение средних скоростей движения воды в канале и сравнение их с максимально допустимыми для заданного грунта скоростями. 10
2. Расчет каналов на неравномерное движение 12
2.1. Определение критической глубины и критического уклона 12
2.2. Построение графика удельной энергии сечения 14
2.4. Построение кривых свободной поверхности на отводящем участке канала 21
3.1. Построение графика прыжковой функции 27
3.2. Построение линии сопряженных
глубин для кривой типа ![]() и
определение местоположения прыжка 28
и
определение местоположения прыжка 28
3.4. Определение длины гидравлического прыжка и потери энергии в нем 29
Поперечное сечение трапецеидального канала, в котором при заданных Q, n, m, i средняя скорость максимальна, а площадь поперечного сечения и смоченный периметр минимальны, называется гидравлически наивыгоднейшим. В строительной практике удобной характеристикой такого сечения является относительная ширина:
(βг.н.)пред. =b/h=2.5+m/2 ; (1.1)
где b-ширина канала по дну; h – глубина потока; m – коэффициент бокового откоса.
Подставляя значение m = 2, 3получим:
(βг.н.)пред. = 2.5 + 2.3/2 = 3.65;
Из геометрических соображений для трапецеидального канала легко найти следующие зависимости:
ширина канала по дну b = ho1(βг.н.)пред. ;
площадь поперечного сечения ω = (b+mh)h;
ширина потока на уровне свободной поверхности B = b+2mh;
смоченный периметр χ = b+2h√1+m2 ;
гидравлический радиус R = ω/ χ;
коэффициент Шези C = R1/6/n;
расход воды Q = ωC√Ri.
Далее для подводящего участка следует найти необходимый
модуль расхода ![]() :
:
![]() ,
,
где ![]() - расход воды в канале, равный 44,2
- расход воды в канале, равный 44,2 ![]() , а
, а ![]() – уклон дна подводящего участка канала, равный
0,0005.
– уклон дна подводящего участка канала, равный
0,0005.
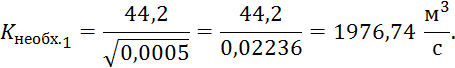
Глубину ![]() равномерного движения на подводящем участке канала
определяем методом подбора. Задаёмся неизвестной величиной и вычисляем все
необходимое. Значение глубины выбираем произвольно. Для удобства построим
таблицу.
равномерного движения на подводящем участке канала
определяем методом подбора. Задаёмся неизвестной величиной и вычисляем все
необходимое. Значение глубины выбираем произвольно. Для удобства построим
таблицу.
|
Величина |
Единицы измерения |
Значения величин |
||||
|
|
|
1 |
1,5 |
2 |
2,5 |
3 |
|
|
|
3,65 |
5,48 |
7,30 |
9,13 |
10,95 |
|
|
|
5,95 |
13,39 |
23,80 |
37,19 |
53,55 |
|
|
|
8,67 |
13,00 |
17,33 |
21,66 |
26,00 |
|
|
|
0,69 |
1,03 |
1,37 |
1,72 |
2,06 |
|
|
|
55,25 |
59,11 |
62,02 |
64,37 |
66,35 |
|
|
|
272,40 |
803,12 |
1729,61 |
3135,99 |
5099,46 |
Пример расчета с ![]()
1. Ширина канала по дну:
![]()
где ![]() – относительная ширина, равная 3,55.
– относительная ширина, равная 3,55.
![]()
2. Площадь живого сечения:
![]()
где ![]() – указанный ранее коэффициент откоса канала, равный
2,1.
– указанный ранее коэффициент откоса канала, равный
2,1.
![]()
3. Смоченный периметр:
![]()
4. Гидравлический радиус:
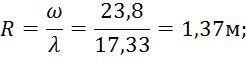
5. Коэффициент Шези:
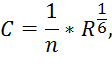
где ![]() – коэффициент шероховатости, равный в данном случае
0,014.
– коэффициент шероховатости, равный в данном случае
0,014.
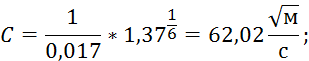
6. Модуль расхода:
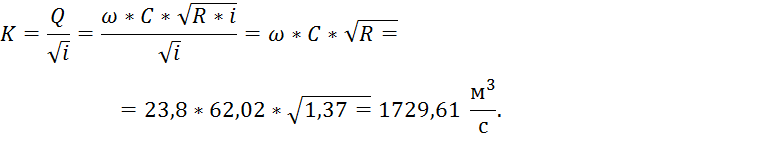
По полученным значениям строим график зависимости нормальной глубины от модуля расхода и на нем, отложим найденный выше необходимый модуль расхода, найдем необходимое значение нормальной глубины (рис.1).
Получили, что ![]()
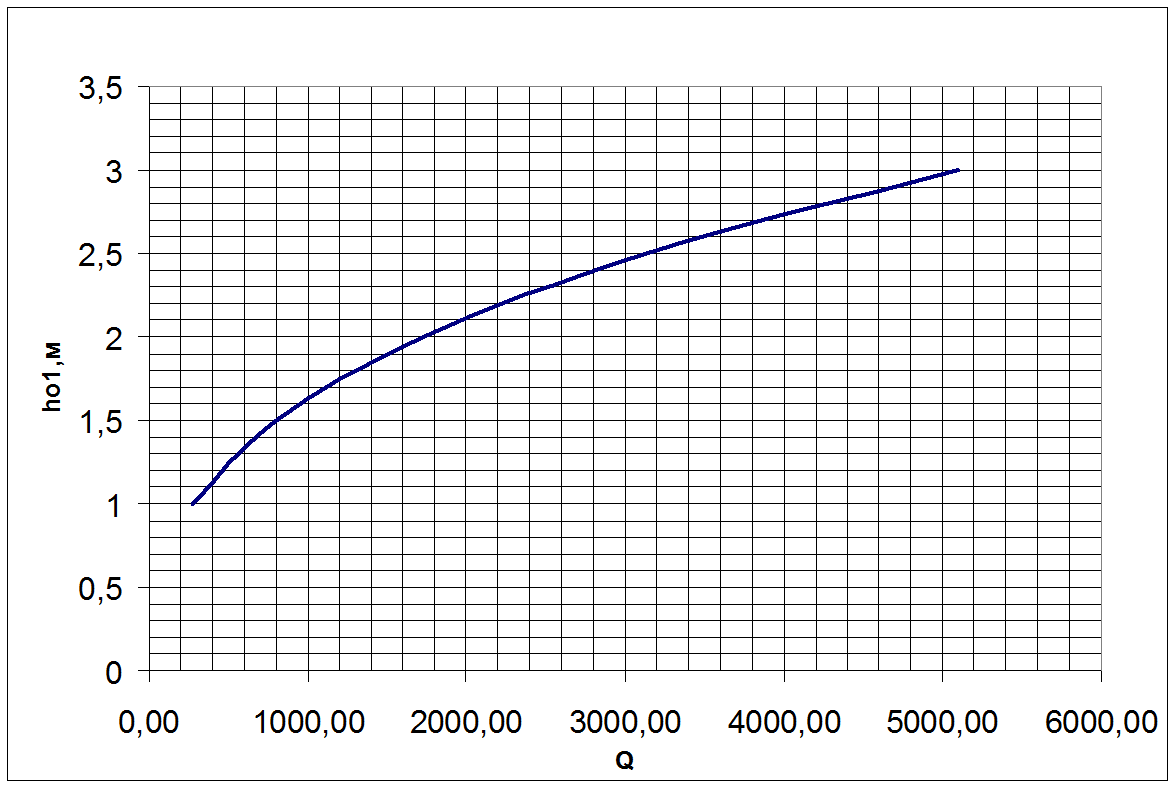
Рис.1 График зависимости нормальной глубины от модуля расхода для подводящего участка
Теперь, зная нормальную глубину на подводящем участке, найдем ширину дна канала на нем:
![]()
Аналогично п.1 заполним таблицу для нахождения ho2 на отводящем участке при b = 7,665 м. Уклон на отводящем участке равен i2 = 0,0002.
Далее для отводящего участка следует найти необходимый модуль расхода ![]() :
:
![]() ,
,
где ![]() - расход воды в канале, равный 44,2
- расход воды в канале, равный 44,2 ![]() ;
;
![]() – уклон дна отводящего участка канала.
– уклон дна отводящего участка канала.
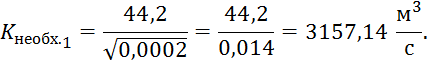
Глубину ![]() равномерного движения на отводящем участке канала
определяем так же методом подбора.
равномерного движения на отводящем участке канала
определяем так же методом подбора.
|
Величина |
Единицы измерения |
Значения величин |
||||
|
|
|
2,0 |
2,5 |
3,0 |
3,5 |
4,0 |
|
|
|
24,53 |
33,54 |
43,70 |
55,00 |
67,46 |
|
|
|
17,70 |
20,20 |
22,71 |
25,22 |
27,73 |
|
|
|
1,39 |
1,66 |
1,92 |
2,18 |
2,43 |
|
|
|
62,11 |
64,01 |
65,60 |
66,99 |
68,22 |
|
|
|
1793,83 |
2765,65 |
3975,78 |
5441,03 |
7178,05 |
Пример расчета с ![]()
1. Площадь живого сечения:
![]()
![]()
2. Смоченный периметр:
![]()
3. Гидравлический радиус:
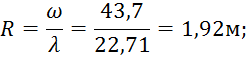
4. Коэффициент Шези:
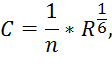
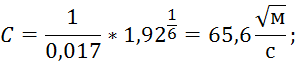
5. Модуль расхода:
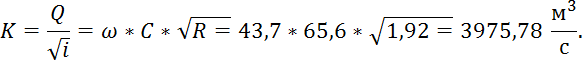
По полученным значениям строим график зависимости нормальной глубины от модуля расхода и на нем, отложим найденный выше необходимый модуль расхода, найдем необходимое значение нормальной глубины на отводящем участке канала (рис.2).
По графику получаем, что нормальная глубина на отводящем участке канала ![]()
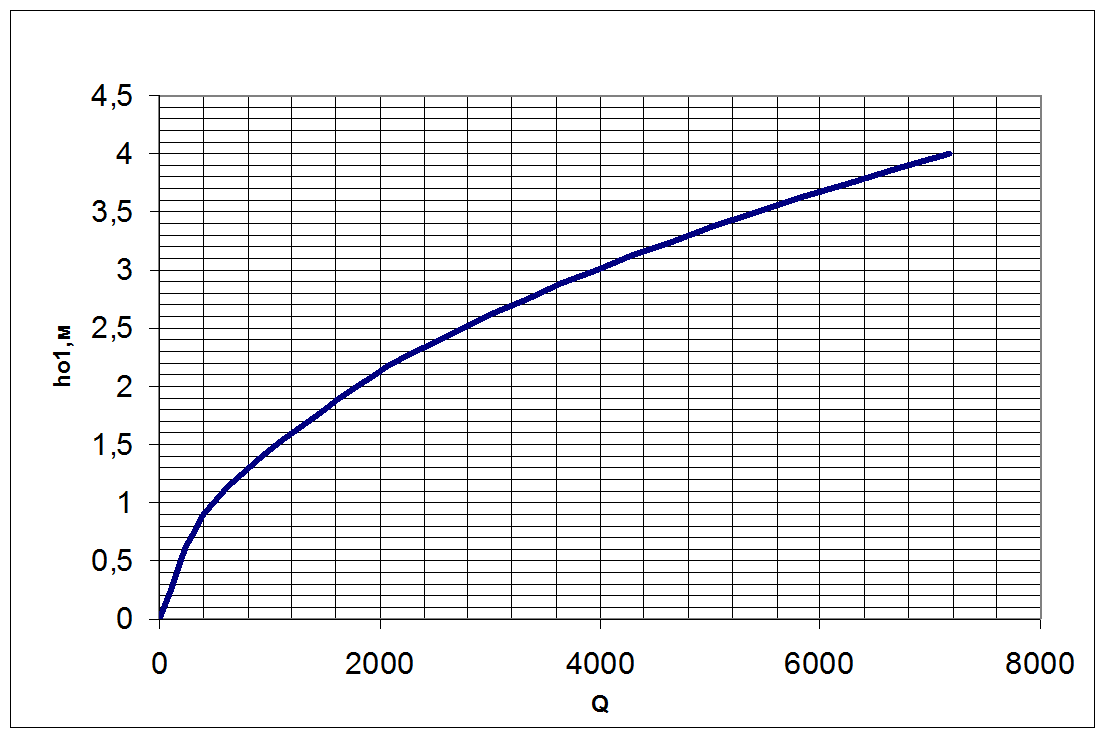
Рис.2 График зависимости нормальной глубины от модуля расхода для отводящего участка
При эксплуатации каналов к скорости воды в них предъявляются два основных требования: она должна лежать в таких пределах, чтобы канал не заилялся и не размывался, то есть должно выполняться неравенство:
(vmin )незаил. < v < (vmax )неразм
Среднюю скорость движения воды в канале определим по формуле:
v = Q/ω.
Подставляя известные значения Q, ω (см. табл.1, 2) получим:
для подводящего участка канала:
v1 = 44,2 / 26,24 = 1,68 м/с,
где ![]()
для отводящего участка канала:
v2 = 44,2 / 36,86 = 1,2 м/с,
где ![]() .
.
Значение (vmax )неразм в общем случае зависит от диаметра частиц слагающих русло канала и глубине потока. В нашем случае при d = 1 мм, ho1 = 2,1 м для подводящего участка и ho2 = 2,67 м для отводящего допустимые неразмывающие скорости соответственно равны:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.