![]()
![]()
Сравнивая значения средних скоростей движения воды в канале с допускаемыми неразмывающими, получаем:
v1> v1 доп. неразм
v2 > v2 доп. неразм
Условие не выполняется ни для одного из участков. Необходимо произвести уменьшение скорости воды в канале.
4. При v>vнеразм. определяем глубину наполнения и уклон дна канала в подводящем канале, полагая v=vнеразм.
Полагаем v1 = v доп.неразм. = 0,59 м/с и находим площадь поперечного сечения ω по формуле:
ω1= Q/ v доп.неразм ;
ω1 = 44,2/ 0,59 = 74,91 м2;
В то же время площадь живого сечения можно найти по формуле:
![]()
Соответственно, приравнивая эти два выражения, получаем квадратное уравнение, из которого можно найти новую нормальную глубину:
![]() ;
;
![]() Для того, чтобы найти уклон, воспользуемся преобразованной формулой
Шези для скорости:
Для того, чтобы найти уклон, воспользуемся преобразованной формулой
Шези для скорости:
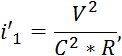
где R (гидравлический радиус) находится по формуле:
![]()
В свою очередь смоченный периметр находится по формуле:
![]() ,
,
а площадь живого сечения:
![]()
Таким образом, получаем:
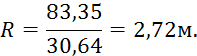
Зная гидравлический радиус, можно найти коэффициент Шези:
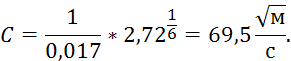
Теперь можем рассчитать уклон:
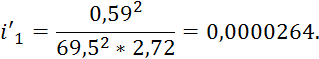
Таким образом, получаем новые значения:
![]()
![]()
![]()
Получившийся профиль представлен на рис. 3
В данном пункте необходимо найти определить критическую глубину hк и критический уклон iк. Вычислим критическую глубину, воспользовавшись следующим уравнением:
![]() ,
,
где α – корректив кинетической
энергии (при турбулентном режиме
принимаем α = 1).
Площадь живого сечения можно определить по формуле:
![]() ,
,
а ширину канала по верху:
B(hk) = b + 2mhk .
Вычислим отношение ![]() :
:
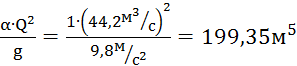 .
.
Определим критическую глубину канала путем подбора:
|
hк |
B |
ω |
|
|
м |
м |
м2 |
м5 |
|
0,8 |
11,35 |
7,60 |
38,75 |
|
1,0 |
12,27 |
9,97 |
80,68 |
|
1,2 |
13,19 |
12,51 |
148,49 |
|
1,4 |
14,11 |
15,54 |
250,90 |
|
1,6 |
15,03 |
18,15 |
398,07 |
Пример расчета таблицы 3 для hк = 1м:
1) hк = 1м;
2) В = 7,665м+2*2,3*1м = 12,27м;
3) ω = (7,665м + 2,3*1м)*1м = 9,97м2;
4) ![]() .
.
По полученным значениям построим
график зависимости (рис.4), при помощи которого можно определить критическую
глубину канала. Из графика видно, что при ![]() , критическая глубина hk =
1,31м.
, критическая глубина hk =
1,31м.
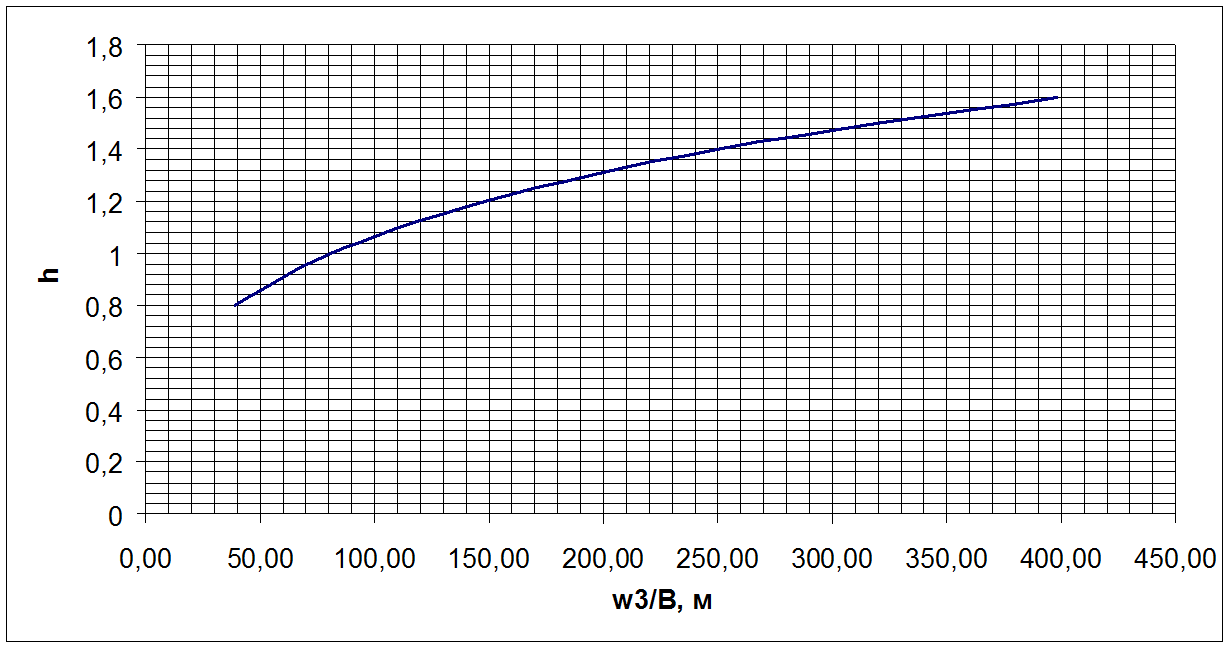
Рис.4. График зависимости глубины канала от w3/B.
Для определения критического уклона воспользуемся формулой:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
В(hk) = b + 2mhk ,
В(hk) = 7,665м + 2*2,3*1,31м = 13,69м ,
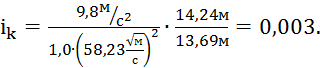 .
.
Таким образом, из проделанных расчетов следует, что критическая глубина канала составляет hk = 1,31м, а критический уклон дна ik = 0,003.
Для построения необходимого графика воспользуемся формулой для вычисления удельной энергии сечения:
![]() ,
,
где ![]() – полная удельная энергия сечения,
м,
– полная удельная энергия сечения,
м,
![]() – удельная потенциальная энергия, м,
– удельная потенциальная энергия, м,
![]() – удельная кинетическая энергия, м.
– удельная кинетическая энергия, м.
Составим таблицу значений, в которой глубины канала будем подбирать произвольно так, чтобы они соответствовали следующим условиям: несколько точек, когда h < hk; когда h = hk; когда h > hk.
|
h |
ω |
υ |
|
Э(h) |
|
м |
м2 |
м/с |
м |
м |
|
0,6 |
5,4 |
8,14 |
3,72 |
4,32 |
|
0,8 |
7,6 |
5,81 |
1,90 |
2,70 |
|
1 |
10,0 |
4,44 |
1,10 |
2,10 |
|
1,2 |
12,5 |
3,53 |
0,70 |
1,90 |
|
1,25 |
13,2 |
3,35 |
0,63 |
1,88 |
|
1,27 |
13,4 |
3,29 |
0,61 |
1,88 |
|
1,29 |
13,7 |
3,22 |
0,58 |
1,87 |
|
1,31 |
14,0 |
3,16 |
0,56 |
1,87 |
|
1,33 |
14,3 |
3,10 |
0,54 |
1,87 |
|
1,35 |
14,5 |
3,04 |
0,52 |
1,87 |
|
1,38 |
15,0 |
2,95 |
0,49 |
1,87 |
|
1,42 |
15,5 |
2,85 |
0,46 |
1,88 |
|
1,5 |
16,7 |
2,65 |
0,39 |
1,89 |
|
1,7 |
19,7 |
2,25 |
0,28 |
1,98 |
|
2 |
24,5 |
1,80 |
0,18 |
2,18 |
|
2,4 |
31,6 |
1,40 |
0,11 |
2,51 |
Пример расчета для h = 0,6м:
1) h = 0,6м;
2) ω = (7,665м + 2,3*0,6м)*0,6м = 5,4м2;
3) ![]() ,
, 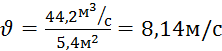 ;
;
4) ![]() ;
;
5) Э(h) = 0,6м + 3,72м = 4,32м.
Теперь по полученным значениям необходимо построить график зависимости глубины канала от удельной энергии сечения.
Таким образом, из графика получили:
Эmin=1,87м.
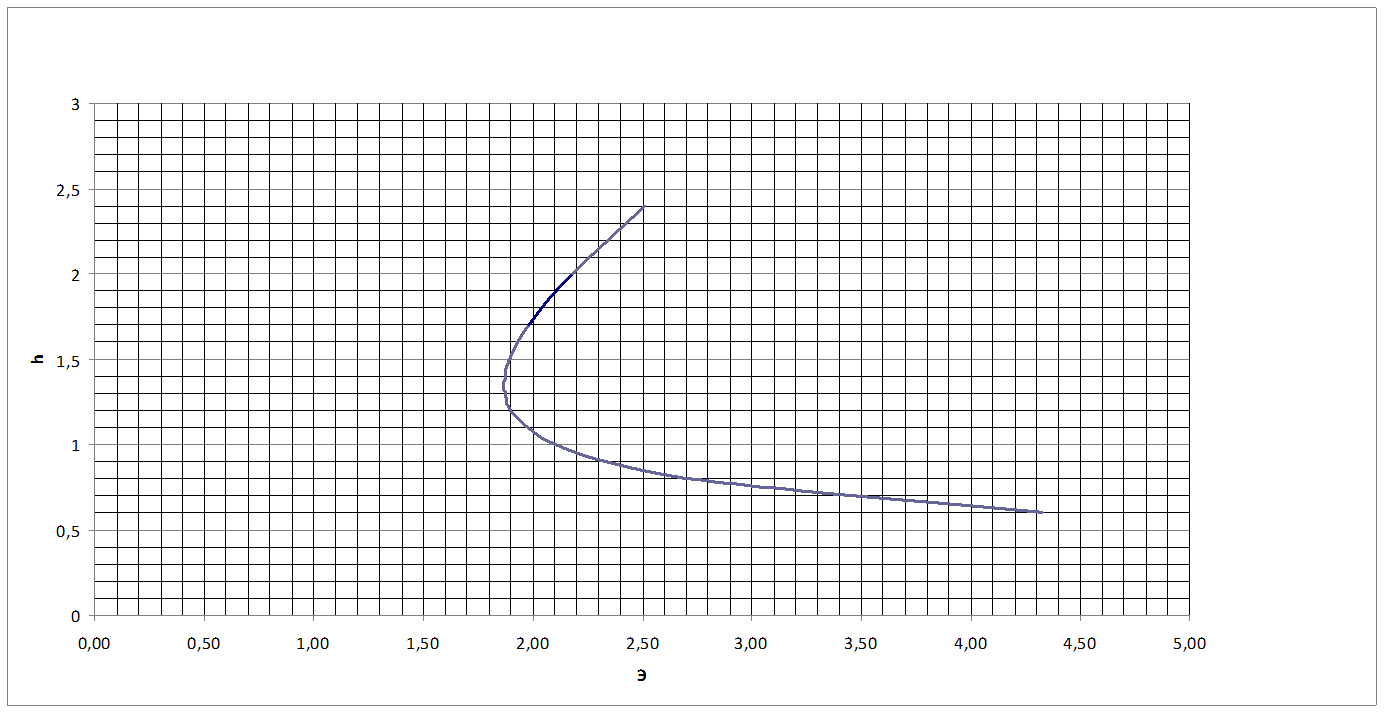
Рис.5. График зависимости удельной энергии от критической высоты
2.3. Построение кривой свободной поверхности на подводящем участке канала
В данном пункте необходимо построить кривую свободной поверхности на подводящем участке канала, пользуясь уравнением Чарномского:
![]() ,
,
где ![]() – длина участка кривой свободной
поверхности между
– длина участка кривой свободной
поверхности между
сечениями m и m+1,
м,
![]() ,
, ![]() – удельные энергии сечений m и m+1 соответственно, м,
– удельные энергии сечений m и m+1 соответственно, м,
i – продольный уклон дна,
![]() – средний уклон трения на
соответствующем участке.
– средний уклон трения на
соответствующем участке.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.