Расчет канала трапецеидального поперечного сечения, страница 4

2.4. Построение кривых свободной поверхности на отводящем участке канала

Построение кривой свободной поверхности типа с_I.

Начальная глубина по заданию принимается при открытии затвора, равной h_нач = 0,63е = 0,63*0,38h_к = 0,2394*1,31 = 0,3136м = h_с. Конечная глубина составляет h_кон = 1,31м.

Шаг, с которым будет рассчитываться глубина, составляет:

 ,

где 5 – число участков,

 .

Составим таблицу зависимости длины участка от глубины канала (аналогично п.2.3).

Пример расчета:

1) h_m+1 = 0,5129м, h_m = 0,3136м;

2) площадь живого сечения:

ω_m+1 = (7,665м + 2,3*0,5129м)*0,5129м = м²,

 ω_m = (7,665м + 2,3*0,3136м)*0,3136 = 2,63м²;

3) скорость движения воды в канале:

  , ;

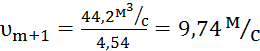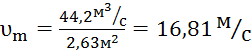4) значение скоростного напора:

  , ;

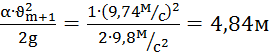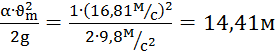5) удельная энергия сечения по формуле Э=h+ :

Э_m+1= 0,5129м + 4,84м = 5,36м,

 Э_m = 0,3136м+ 14,41 = 14,72м;

6) разность удельных энергий:

Э_m+1 – Э_m = 5,36-14,72м = -9,37м;

7) средняя глубина между поперечными сечениями:

  ;

8) средняя площадь живого сечения:

  ;

9) средний смоченный периметр:

  ;

10) гидравлический радиус

  ;

11) коэффициент Шези:  ;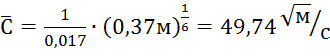

12) средний уклон:   ;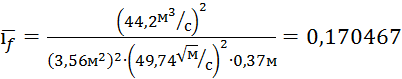

13) разность уклона подводящего участка и среднего уклона:

 ;

14) расстояние между поперечными сечениями канала по уравнению Чарномского:

 .

Таким образом, суммарная длина подводящего участка : l=м.

По получившимся результатам можно построить кривую свободной поверхности типа с_I (рис.7).

Построение кривой свободной поверхности типа b_I.

Имеется только одна глубина – это критическая глубина канала h_к, которая принимается как начальная глубина h_m. Конечная глубина не известна, следовательно, посчитать шаг по глубине невозможно. Первый шаг примем близким шагу для кривой типа a_I (Δh₁ = 0,5). Последующие шаги берутся в зависимости от полученных значений длин участков. В данном случае рассматривается шесть участков. Последняя глубина должна быть как можно ближе к щиту. 

Составим таблицу зависимости длины участка от глубины канала.

Пример расчета для глубины h_m+1 = 1,31м и h_m = 1,81м:

1) h_m+1 = 1,31м, h_m = 1,81м;

2) ω_m+1 = (7,665м + 2,3*1,31м)*1,31м = 13,99м²,

    ω_m = (7,665м + 2,3*1,81м)*1,81м = 21,41м²;

3) , ;

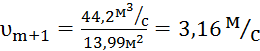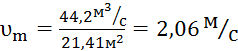4) , ;

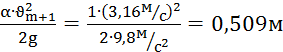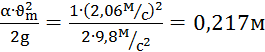5) Э_m+1 = 1,31м + 0,509м = 1,82м,

    Э_m = 1,81м + 0,217м = 2,03м;

6) Э_m+1 – Э_m = 1,82м – 2,03м = - 0,21м;

7)  ;

8)  ;

9)  ;

10)  ;

11)  ;

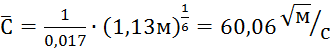12)  ;

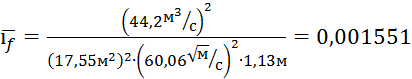13)  ;

14)  .

По результатам можно построить кривую свободной поверхности типа b_I (рис.7).