![]()
Гидравлическим прыжком называется явление резкого увеличения глубины от ![]() до
до ![]() , при котором поток из бурного
состояния переходит в спокойное. Глубины h’ и h’’ называются сопряженными, h’ – первой, а h’’ – второй сопряженной глубиной. При этом явлении
энергия вдоль потока уменьшается.
, при котором поток из бурного
состояния переходит в спокойное. Глубины h’ и h’’ называются сопряженными, h’ – первой, а h’’ – второй сопряженной глубиной. При этом явлении
энергия вдоль потока уменьшается.
Прыжковая функция имеет следующий вид:
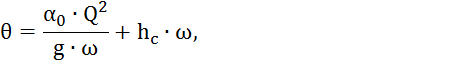
где ![]() - корректив количества
движения;
- корректив количества
движения; ![]() - координата центра
тяжести данного живого сечения канала, м.
- координата центра
тяжести данного живого сечения канала, м.
Координата центра тяжести ![]() определяется по формуле:
определяется по формуле:
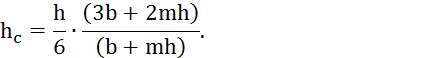
Далее для различных значений глубин наполнения канала определяются значения прыжковой функции. Вычисленные данные сводятся в таблицу.
|
|
|
|
hc |
|
|
|
|
м |
м2 |
М |
м3 |
|||
|
1 |
0,6 |
5,4 |
0,28 |
1,545 |
36,696 |
38,2 |
|
2 |
0,8 |
7,6 |
0,37 |
2,845 |
26,189 |
29,0 |
|
3 |
1 |
10,0 |
0,46 |
4,599 |
19,985 |
24,6 |
|
4 |
1,2 |
12,5 |
0,55 |
6,8434 |
15,919 |
22,8 |
|
5 |
1,25 |
13,2 |
0,57 |
7,486 |
15,116 |
22,6 |
|
6 |
1,27 |
13,4 |
0,58 |
87,752 |
14,813 |
22,6 |
|
7 |
1,29 |
13,7 |
0,59 |
8,023 |
14,52 |
22,5 |
|
8 |
1,31 |
14,0 |
0,59 |
8,3 |
14,237 |
22,5 |
|
9 |
1,33 |
14,3 |
0,60 |
8,583 |
13,963 |
22,5 |
|
10 |
1,35 |
14,5 |
0,61 |
8,871 |
13,697 |
22,6 |
|
11 |
1,38 |
15,0 |
0,62 |
9,313 |
13,314 |
22,6 |
|
12 |
1,42 |
15,5 |
0,64 |
9,923 |
12,83 |
22,8 |
|
13 |
1,5 |
16,7 |
0,67 |
11,211 |
11,945 |
23,2 |
|
14 |
1,7 |
19,7 |
0,75 |
14,843 |
10,121 |
25,0 |
|
15 |
2,00 |
24,53 |
0,87 |
21,46 |
8,12 |
29,58 |
|
16 |
2,70 |
37,46 |
1,15 |
43,03 |
5,32 |
48,35 |
Пример расчета строки таблицы для ![]()
1) площадь живого сечения:
![]()
2) координата центра тяжести живого сечения канала:
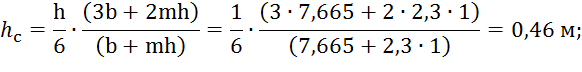
3) 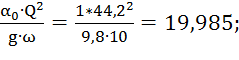
4) ![]() м3;
м3;
5) прыжковая функция по формуле:
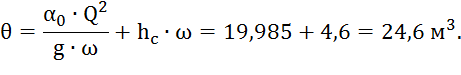
По данным таблицы строится график зависимости прыжковой функции от глубины воды в канале (см. рис. 8).
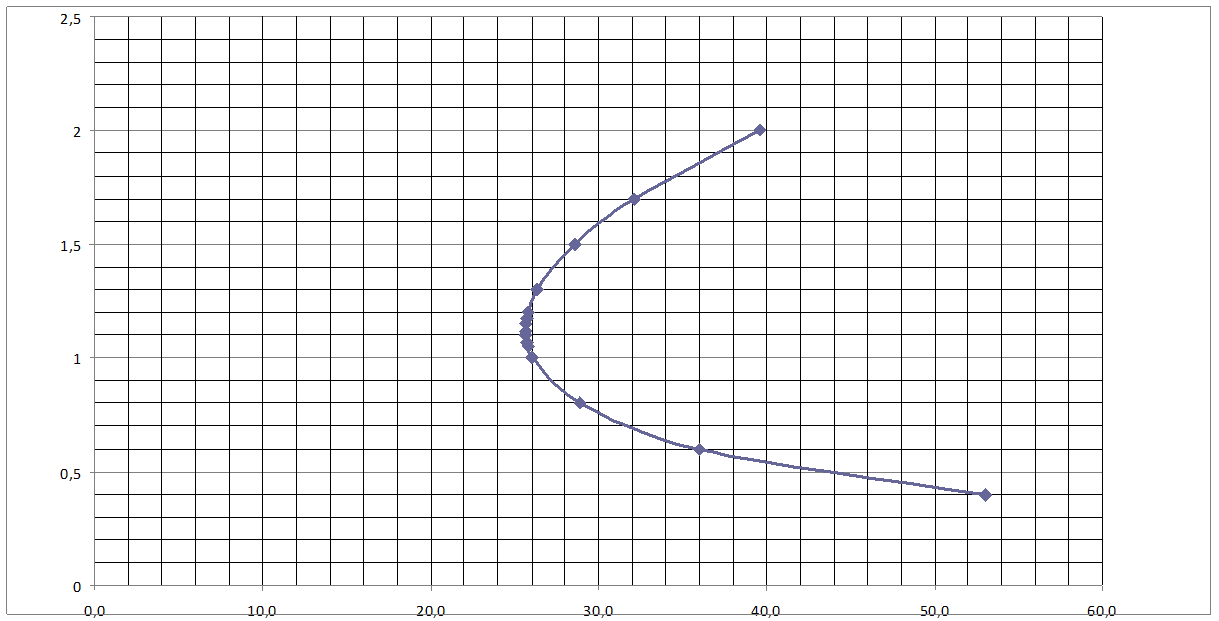
Рис.8. График зависимости прыжковой функции от глубины воды в канале
Кривая типа ![]() является линией возможных первых
сопряженных глубин
является линией возможных первых
сопряженных глубин ![]() . Зная первые сопряженные глубины, по
графику прыжковой функции
. Зная первые сопряженные глубины, по
графику прыжковой функции ![]() ) (см. рис. 8), определяются вторые
сопряженные глубины
) (см. рис. 8), определяются вторые
сопряженные глубины ![]() . Полученные результаты записываются в
таблицу.
. Полученные результаты записываются в
таблицу.
|
№ |
|
|
|
1 |
0,3136 |
3,3 |
|
2 |
0,5129 |
2,58 |
|
3 |
0,7122 |
2,08 |
|
4 |
0,9115 |
1,82 |
|
5 |
1,1108 |
1,54 |
|
6 |
1,31 |
1,31 |
Полученные значения вторых
сопряженных глубин откладываются на рис. 7, где изображены кривые свободной
поверхности. Построенная кривая является линией вторых сопряженных глубин. В
точке пересечении линии вторых сопряженных глубин и линии свободной поверхности
типа ![]() находится
гидравлический прыжок и соответствующие ему первая и вторая сопряженные
глубины:
находится
гидравлический прыжок и соответствующие ему первая и вторая сопряженные
глубины:
![]()
![]()
Высота гидравлического прыжка высчитывается как разность сопряженных глубин:
![]()
Для определения длины гидравлического прыжка имеется эмпирическая зависимость:
![]()
Потеря энергии в пряжке находится по формуле:
![]()
Рассмотрим уменьшаемое и вычитаемое отдельно.
1. Удельная энергия, соответствующая первой сопряженной глубине:
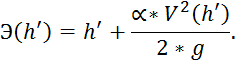
Чтобы найти скорость, сначала необходимо найти площадь живого сечения:
![]()
Таким образом, скорость равна:
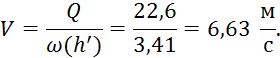
Теперь можем найти значение удельной энергии сечения:
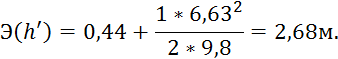
2. Удельная энергия, соответствующая второй сопряженной глубине:
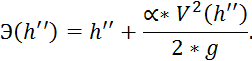
Чтобы найти скорость, сначала необходимо найти площадь живого сечения:
![]()
Таким образом, скорость равна:
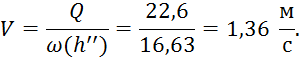
Теперь можем найти значение удельной энергии сечения:
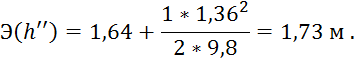
Потеря энергии в прыжке:
![]()
Схема гидравлического прыжка с нанесением напорной линии представлена на рис. 8.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.