Санкт-Петербургский государственный политехнический университет
Инженерно-строительный факультет
Кафедра гидравлики
Расчетно-графическая работа № 4
по курсу гидравлики
Выполнил: Савченко Д.Б., группа 3013/1
Проверила: Локтионова Е.А.
Санкт-Петербург
2012
Оглавление
1. ОПРЕДЕЛЕНИЕ ГЛУБИНЫ РАВНОМЕРНОГО ДВИЖЕНИЯ h01 И ШИРИНЫ КАНАЛА ПО ДНУ b НА ПОДВОДЯЩЕМ УЧАСТКЕ КАНАЛА ПРИ β=(βГ.Н.)ПРЕД. 3
1.1. Глубина равномерного движения h01 3
1.2. Ширина канала по дну b. 4
2. ОПРЕДЕЛЕНИЕ ГЛУБИНЫ РАВНОМЕРНОГО ДВИЖЕНИЯ h02НА ОТВОДЯЩЕМ УЧАСТКЕ КАНАЛА.. 6
3. ОПРЕДЕЛЕНИЕ СРЕДНИХ СКОРОСТЕЙ ДВИЖЕНИЯ ВОДЫ В КАНАЛЕ И СРАВНЕНИЕ ИХ С МАКСИМАЛЬНО ДОПУСТИМЫМИ ДЛЯ ЗАДАННОГО ГРУНТА СКОРОСТЯМИ.. 11
4. ОПРЕДЕЛЕНИЕ КРИТИЧЕСКОЙ ГЛУБИНЫ hK И КРИТИЧЕСКОГО УКЛОНА iK КАНАЛА.. 15
4.1. Определение критической глубины hК. 15
4.2. Определение критического уклона iК. 16
5. ПОСТРОЕНИЕ ГРАФИКА УДЕЛЬНОЙ ЭНЕРГИИ СЕЧЕНИЯ.. 18
6. ПОСТРОЕНИЕ КРИВОЙ СВОБОДНОЙ ПОВЕРХНОСТИ НА ПОДВОДЯЩЕМ УЧАСТКЕ КАНАЛА.. 20
7. ПОСТРОНИЕ КРИВЫХ СВОБОДНОЙ ПОВЕРХНОСТИ ТИПА СI И BI НА ОТВОДЯЩЕМ УЧАСТКЕ КАНАЛА.. 25
7.1. Кривая свободной поверхности типа сI 25
7.2. Кривая свободной поверхности типа bI 28
8. ПОСТРОЕНИЕ КРИВЫХ СВОБОДНОЙ ПОВЕРХНОСТИ НА ПОДВОДЯЩЕМ И ОТВОДЯЩЕМ УЧАСТКАХ КАНАЛА ПРИ ПОЛНОСТЬЮ ОТКРЫТОМ ЗАТВОРЕ. 33
9. ПОСТРОЕНИЕ ГРАФИКА ПРЫЖКОВОЙ ФУНКЦИИ θ(h) 35
10. ПОСТРОЕНИЕ ЛИНИИ СОПРЯЖЁННЫХ ГЛУБИН ДЛЯ КРИВОЙ ТИПА СIИ ОПРЕДЕЛЕНИЕ МЕСТОПОЛОЖЕНИЯ ГИДРАВЛИЧЕСКОГО ПРЫЖКА.. 38
11. ОПЕРЕДЕЛЕНИЕ ПАРАМЕТРОВ ГИДРАВЛИЧЕСКОГО ПРЫЖКА.. 38
ЛИТЕРАТУРА.. 41
Определим предельное значение относительной ширины канала β.
![]() , (1.1)
, (1.1)
где m – коэффициент откоса канала (m=2).
![]() .
.
Найдём необходимое значение модуля расхода Кнеобх1.
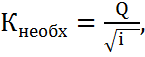 (1.2)
(1.2)
где Q – расход воды в канале (Q = 52,7 м3/с);
i – уклон дна на соответствующем участке канала (i1 = 0,0001).
![]() м3/с.
м3/с.
Зная значение необходимого модуля расхода определим глубину канала h01. Для этого составим таблицу, отражающую зависимость модуля расхода от глубины канала (табл. 1.1).
Таблица 1.1
|
h01 |
м |
2,00 |
2,5 |
3,0 |
3,20 |
3,50 |
|
b |
м |
7,00 |
8,75 |
10,50 |
11,2 |
12,25 |
|
ω |
м2 |
22,00 |
34,38 |
49,50 |
56,32 |
67,38 |
|
χ |
м |
15,94 |
19,93 |
23,92 |
25,51 |
27,90 |
|
R |
м |
1,38 |
1,72 |
2,07 |
2,21 |
2,41 |
|
C |
м1/2/с |
62,07 |
64,42 |
66,41 |
67,12 |
68,13 |
|
K1 |
м3/с |
1603,93 |
2908,12 |
4728,93 |
5617,02 |
7133,25 |
Пример расчёта таблицы (для h01= 2м):
1. Ширина канала:
![]() (1.3)
(1.3)
b = 3,5 * 2 = 7 м.
2. Площадь живого сечения канала:
![]() . (1.4)
. (1.4)
ω = (7 + 2 * 2) * 2 = 22 м2.
3. Смоченный периметр живого сечения канала:
![]() . (1.5)
. (1.5)
![]() .
.
4. Гидравлический радиус:
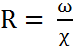 . (1.6)
. (1.6)
![]() м.
м.
5. Коэффициент Шези:
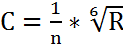 , (1.7)
, (1.7)
где n – коэффициент шероховатости (n = 0,017).
![]()
![]() /с.
/с.
6. Модуль расхода:
Модуль расхода определяется по формуле (1.2). Сам расход может быть найден по формуле:
![]() . (1.8)
. (1.8)
Используя формулы (1.2) и (1.8) выразим модуль расхода иначе:
![]() (1.9)
(1.9)
![]() м3/с.
м3/с.
По данным таблицы 1.1 строим график зависимости h01 =h0(K1) (рис.1.1). Используя этот график определим значение глубины канала на подводящем участке. Это значение будет равно значению глубины, соответствующей необходимому модулю расхода.
Kнеобход1 =
![]() м3/с
=>h01 = 3,15
м.
м3/с
=>h01 = 3,15
м.
Ширина канала определяется по формуле (1.3):
b = 3,5 * 3,15 = 11,03 м.
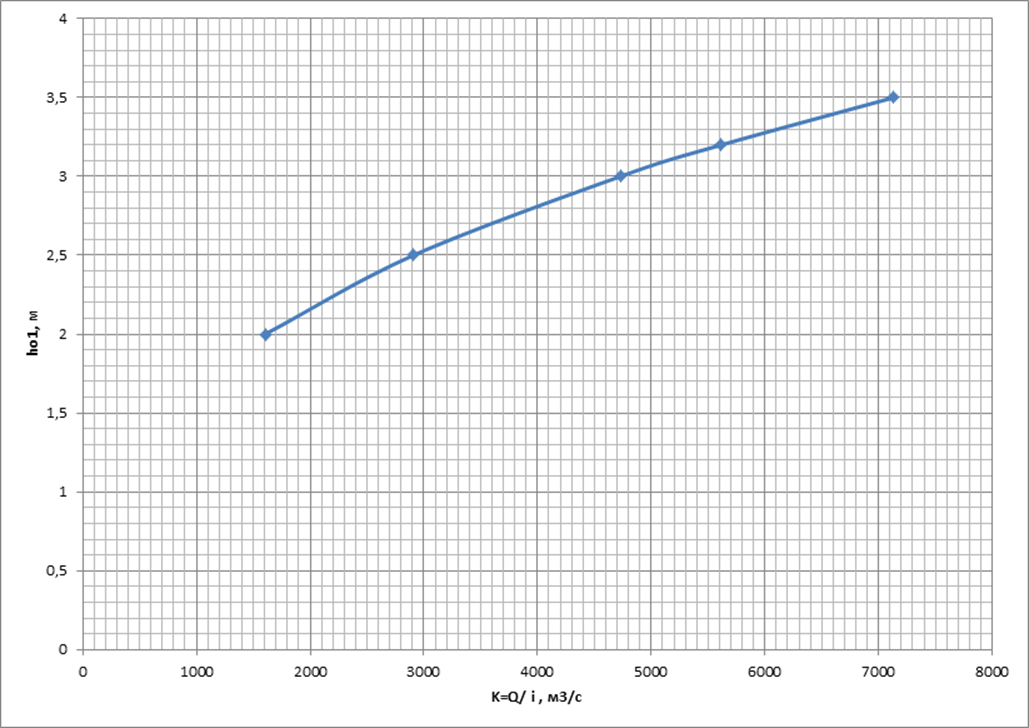
Рис. 1.1. График зависимости глубины равномерного движения от величины модуля расхода для подводящего участка
Полагаем, что ширина канала равна найденной в п. 1.2, т.е b= 11,03 м.
Аналогично п.1.1 найдём необходимое значение модуля расхода Кнеобх2 по формуле (1.2) (i2 = 0,5 * i1 = 1,3 * 0,0001 = 0,00013):
![]() м3/с.
м3/с.
Так же, как в п.1.1 составим таблицу, отражающую зависимость модуля расхода от глубины канала (табл 2.1).
Таблица 2.1
|
h02 |
м |
2,00 |
2,50 |
3,00 |
3,20 |
3,50 |
|
b |
м |
11,03 |
11,03 |
11,03 |
11,03 |
11,03 |
|
ω |
м2 |
30,06 |
40,08 |
51,09 |
55,78 |
63,11 |
|
χ |
м |
19,97 |
22,21 |
24,45 |
25,34 |
26,68 |
|
R |
м |
1,50 |
1,80 |
2,09 |
2,20 |
2,37 |
|
C |
м1/2/с |
62,97 |
64,90 |
66,51 |
67,09 |
67,90 |
|
K2 |
м3/с |
2322,12 |
3493,84 |
4912,48 |
5551,57 |
6589,31 |
Пример расчёта таблицы (для h02= 2м):
1. Ширина канала:
b = 11,03 м.
2. Площадь живого сечения канала:
по формуле (1.4):
ω = (11,03+ 2 * 2) * 2 = 30,06 м2.
3. Смоченный периметр живого сечения канала:
по формуле (1.5):
![]() м.
м.
4. Гидравлический радиус:
по формуле (1.6):
![]() м.
м.
5. Коэффициент Шези:
по формуле (1.7):
![]() /с.
/с.
6. Модуль расхода:
по формуле (1.9):
![]() м3/с.
м3/с.
По данным таблицы 2.1 строим график зависимости h02= h0(K2) (рис.2.1). Используя этот график определим значение глубины канала на отводящем участке. Это значение будет равно значению глубины, соответствующей необходимому модулю расхода.
Kнеобход2 =
![]() м3/с
=>h02 = 2,9 м.
м3/с
=>h02 = 2,9 м.
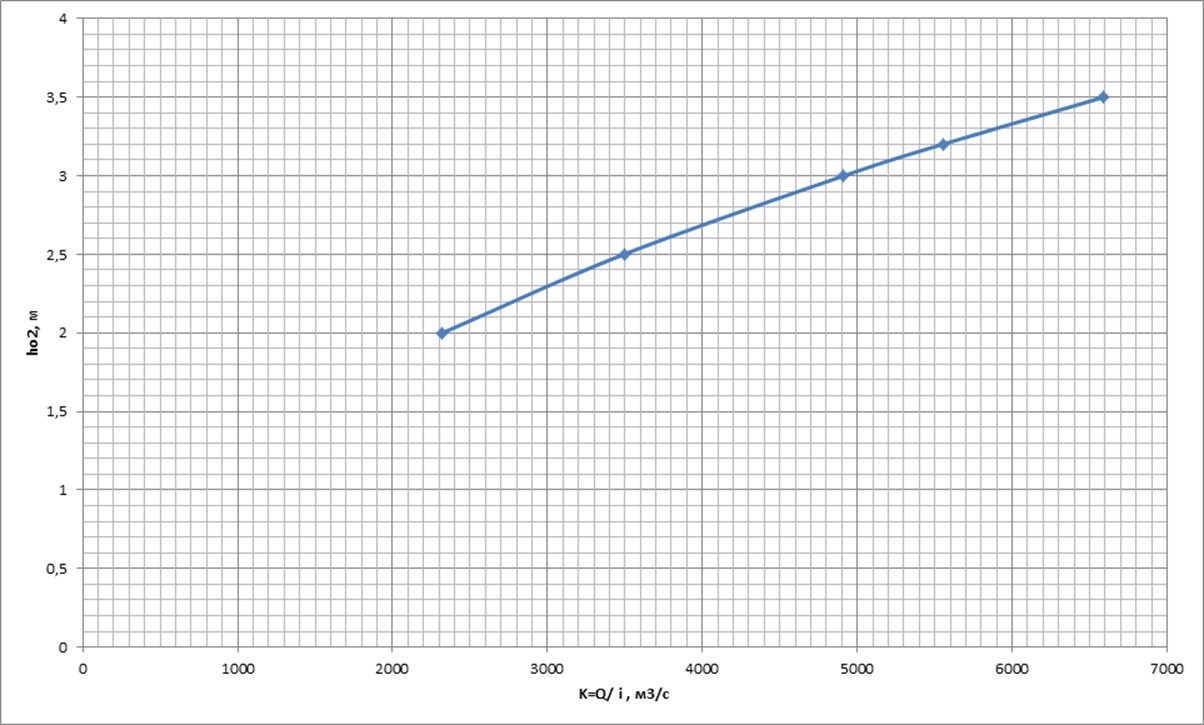
Рис. 2.1. График зависимости глубины равномерного движения от величины модуля расхода для отводящего участка
На рис. 2.2 показаны сечения канала на отводящем и подводящем участке канала.
Ширина канала по верху определяется по формуле:
![]() . (2.1)
. (2.1)
- на подводящем участке:
B = 11,03+ 2 * 2 * 3,15 = 23,63 м;
- на отводящем участке:
B = 11,03+ 2 * 2 * 2,9 = 22,63 м.
Необходимо осуществить проверку полученных глубин канала.
Т.к. i1 < i2, то должно выполняться условие h01 > h02.
h01 = 3,15 м > h02 = 2,9 м => условие выполнено.
Средняя скорость движения воды в канале определяется по формуле:
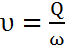 . (3.1)
. (3.1)
Найдём площади живого сечения канала по формуле (1.4):
- на подводящем участке:
ω = (11,03 + 2 * 3,15)*3,15 = 54,59 м2;
- на отводящем участке:
ω = (11,03 + 2 * 2,9)*2,9 = 48,80 м2.
Используя формулу (3.1) найдём средние скорости движения воды на обоих участках канала:
- на подводящем участке:
![]() .
.
- на отводящем участке:
![]() .
.
Максимально допустимая скорость является функцией диаметра частиц грунта, слагающего русло канала, и глубины канала: (υmax)неразм=f(d, h0).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.