Решение плоской задачи фильтрации воды под гидротехническим сооружением

Санкт-Петербургский государственный политехнический университет

Инженерно-строительный факультет

Кафедра гидравлики

Расчетно-графическое задание №3

Дисциплина: Гидравлика

Тема: Решение плоской задачи фильтрации воды под гидротехническим сооружением

Выполнил студент группы 3013/1             Шепетько В.В.

     Преподаватель                                         Локтионова Е.А.

«_____»______________2011г.

Санкт-Петербург

2011

Оглавление

1. Решение фильтрационной задачи методом электрогидродинамической аналогии (ЭГДА) 4

2. Решение фильтрационной задачи методом коэффициентов сопротивления (МКС) 6

3. Сравнение результатов расчета. 11

Литература. 13

1. Решение фильтрационной задачи методом электрогидродинамической аналогии (ЭГДА)

1) После проделывания лабораторной работы необходимо перенести линии приведенного потенциала (H_r = const) на миллиметровку.

2) Присвоить линиям H_r = const действительные наименования.

H_ri = 1; 0,9; 0,8; 0,7; 0,6; 0,5; 0,4; 0,3; 0,2; 0,1; 0.

H_i = h₂ + Z·H_ri ,

Z = h₁ – h₂ ,           Z = 11,3м – 2,9м = 8,4м.

H₁ = h₂ + z·1,       H₁ = 2,9м + 8,4м·1 = 11,3м.

H₂ = h₂ + z·0,9 ,   H₂ = 2,9м + 8,4м·0,9 = 10,46м.

H₃ = h₂ + z·0,8 ,   H₃ = 2,9м + 8,4м·0,8 = 9,62м.

H₄ = h₂ + z·0,7 ,   H₄ = 2,9м + 8,4м·0,7 = 8,78м.

H₅ = h₂ + z·0,6 ,   H₅ = 2,9м + 8,4м·0,6 = 7,94м.

H₆ = h₂ + z·0,5 ,   H₆ = 2,9м + 8,4м·0,5 = 7,1м.

H₇ = h₂ + z·0,4 ,   H₇ = 2,9м + 8,4м·0,4 = 6,26м.

H₈ = h₂ + z·0,3 ,   H₈ = 2,9м + 8,4м·0,3 = 5,42м.

H₉ = h₂ + z·0,2 ,   H₉ = 2,9м + 8,4м·0,2 = 4,58м.

H₁₀ = h₂ + z·0,1 ,  H₁₀ = 2,9м + 8,4м·0,1 = 3,74м.

H₁₁ = h₂ + z·0 ,     H₁₁ = 2,9м + 8,4м·0 = 2,9м.

3) Необходимо провести на глаз и от руки три промежуточных линии тока, добиваясь ортогональности сетки. Для этого лучше начать с участка, где движение практически равномерное. Делим на четыре участка, и начинаем проводить линии сверху вниз.

4)Теперь следует построить эпюру противодавления. Вычислить силу противодавления (F).

Для начала необходимо найти характерные точки подземного контура (в данном случае их шесть). Затем, наметить плоскость сравнения по линии дна и отложить значения напора в каждой характерной точке (потери напора на каждом элементе подземного контура).

h_вх = H₍₁₎ – H₍₂₎ ,

h_г1 = H₍₂₎ – H₍₃₎ ,

h_ш = H₍₃₎ – H₍₄₎ ,

h_г2 = H₍₄₎ – H₍₅₎ ,

h_вых = H₍₅₎ – H₍₆₎ .

В угловых точках, куда не подошли линии равного напора, необходимо произвести пересчет потенциалов в действительные значения на поров по формуле:

H_i = h₂ + Z·H_ri.

H₍₁₎ = H₁ = 11,3м.

H₍₂₎ = H₂ = 10,46м.

H₍₃₎ = 2,9м + 8,4м·0,766 = 9,33м.

H₍₄₎ = 2,9м + 8,4м·0,475 = 6,89м.

H₍₅₎ = 2,9м + 8,4м·0,343 = 5,78м.

H₍₆₎ = H₁₁ = 2,9м.

Получаем:

h_вх = 11,3м – 10,46м = 0,84м,

h_г1 = 10,46м – 9,33м = 1,13м,

h_ш = 9,33м – 6,89м = 2,44м,

h_г2 = 6,89м – 5,78м = 1,11м,

h_вых = 5,78м – 2,9м = 2,88м.

Эпюра противодавления – это все, что ограничено вертикалями, свободной поверхностью и самой поверхностью, а также бетон.

Сила противодавления вычисляется по формуле:

F = A_эп·b·γ,

где A_эп – площадь эпюры противодавления,

      b = 1м, γ = 10⁴Н/м³.

F = 166,08м²·1м·10⁴Н/м³ = 1660,8кН.

5) Необходимо определить выходной градиент (J_вых) и выходную скорость фильтрации (V_вых).

V_вых = k·J_вых.

Наметим несколько точек (в данной работе 7 точек) вдоль линии дна нижнего бьефа.

Для определения градиента воспользуемся формулой:

 ,

где ΔН – разность напоров между ближайшими к данной точке линиями  

                равных потенциалов (ΔН=0,84м),

      Δl_i – отрезок промежуточной линии тока, проведенной через данную  

              точку между линиями Н₁₀ и Н₁₁.

Составим таблицу (табл.1) для определения выходного ингредиента и скорости.

Таблица 1

№ точек	Δl, м	J	V, м/с
I	4,6	0,183	21,96·10-8
II	4,8	0,175	21·10-8
III	5,0	0,168	20,16·10-8
IV	5,6	0,15	18·10-8
V	6,2	0,135	16,2·10-8
VI	7,0	0,12	14,4·10-8
VII	8,4	0,1	12·10-8

Пример расчета для I точки:

1) Δl = 4,6м.

2)  .

3) V = 1,2·10^-6м/с·0,18 = 21,96·10^-8м/с.

По полученным значениям скоростей необходимо построить эпюру выходных скоростей.

6) Необходимо определить удельный фильтрационный расход (q). Для этого выбираем две соседние линии равного напора, где движение близко к плавно изменяющемуся, которые начинаясь на подземном контуре заканчиваются на водоупоре. Выделим расчетные отсеки и составим таблицу (табл.2).

Таблица 2

№ отсека	Δl, м	J=	V, м/с	Δω, м	Δq= V· Δω, м2/с
I	4,6	0,183	2,2·10-7	4,3	9,46·10-7
II	6	0,14	1,68·10-7	5,4	9,07·10-7
III	7,4	0,114	1,37·10-7	5,6	7,67·10-7
IV	8	0,105	1,26·10-7	5,0	6,3·10-7
					32,5·10-7

Пример расчета для I отсека:

1) Δl = 4,6м.

2)  .

3) V = 1,2·10^-6м/с·0,183 = 2,2·10^-7м/с.

4) Δω = 4,3м.

5) Δq = 2,2·10^-7м/с·4,3м = 9,46·10^-7м²/с.

q = ∑ Δq = 32,5·10^-7м²/с.

Все пункты изображены на рис.1.

2. Решение фильтрационной задачи методом коэффициентов сопротивления (МКС)

Идея МКС состоит в том, что напорное резко изменяющееся движение между подземным контуром и водоупором рассматривается как движение в трубе, заполненной водопроницаемым грунтом. На элементах подземного контура имеют место потери напора, каждую из которых можно представить как часть полного напора Z. Коэффициенты сопротивления ζ_j, которые показывают какую часть полного напора Z составляют потери на каждом элементе, зависят от геометрических размеров элемента. При этом полагают, что элементы не влияют друг на друга, и коэффициенты ζ_j можно складывать.

Схема расчета по МКС:

1) Выделить характерные типовые элементы подземного контура.

2) Составить расчетную зависимость для каждого элемента и вычислить все ζ_j.

3) Найти суммарный коэффициент сопротивления ∑ ζ_j.

4) Решить три фильтрационные задачи:

            - определить силу противодавления F;

            - вычислить максимальный выходной градиент (J_вых)_max и максимальную выходную скорость (V_вых)_max.

            - определить удельный фильтрационный расход q.

Метод коэффициентов сопротивления построен таким образом, что формулы для ζ_j одинаковы, но в зависимости от решаемой задачи каждый раз заново приходится назначать вертикальный размер трубы. В этой связи вводят понятие глубины активной зоны фильтрации (Т_ак). Это предельное заглубление водоупора, до которого рассматриваемая величина изменяется, а при дальнейшем заглублении водоупора ее изменения не существенны.

Существует также глубина активной зоны по напору - Т_ак’ и глубина активной зоны по выходному градиенту - Т_ак’’. Глубина Т_ак’’’ принимается равной действительному заглублению водоупора Т_д. Также рассматривается понятие как расчетное положение водоупора – Т_расч [Т_расч = min(Т_д, Т_ак)].

 ,

где l_o – горизонтальная проекция подземного контура,

      S_o – вертикальная проекция подземного контура (до самого длинного 

             шпунта).

В данной работе l_o=30,8м, S_o=13,2м. Отношение .

При  → Т_ак’= 0,8· S_o + 0,5· l_o .

Т_ак’= 0,8·13,2м + 0,5·30,8м = 25,96м.

Т_ак’’=2·Т_ак’,

Т_ак’’=2·25,96м = 51,92м.

Т_д = 30,8м (из схемы).

Т_расч’ = Т_ак’ = 25,96м,

(Т_расч” = Т_д = 30,8м).

Расчетные зависимости для коэффициентов сопротивления.

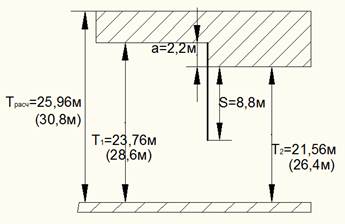Внутренний шпунт

 ,

 ,

 .

 .

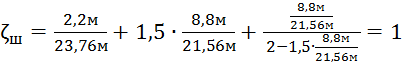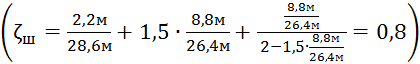Вход

,

 .

 .

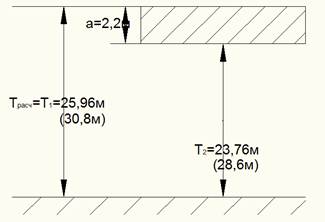
Выход

 ,

 .

.

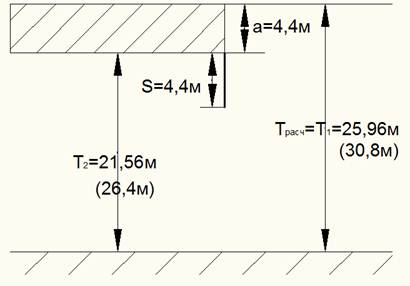
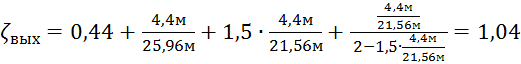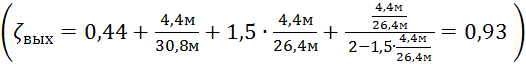Горизонтальные элементы

 ,

,

 . .

 ,

 . .

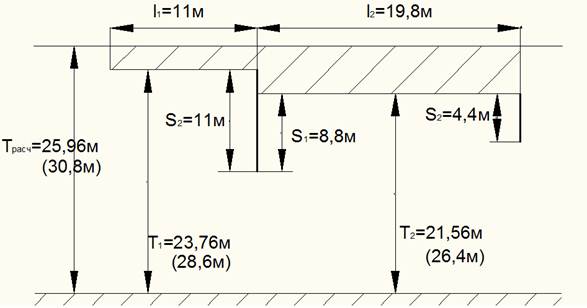
Решение фильтрационных задач:

1) Построение эпюры противодавления и вычисление силы F.

 .

При  → Т_ак’= 0,8· S_o + 0,5· l_o .

Т_ак’= 0,8·13,2м + 0,5·30,8м = 25,96м.

Т_д = 30,8м (из схемы).

Т_расч’ = Т_ак’ = 25,96м.

 ,

 ,

 ,

 ,

 .

Полный коэффициент сопротивления составляет:

ζ_f’=∑ζ_j = 0,52+1+0,23+0,61+1,04=3,4.

Потери напора на каждом элементе:

 ,

 ,

 ,

 ,

 ,

 .

∑h_j = (1,28+0,57+2,47+1,51+2,57)м = 8,4м = z.

F = 169,95м²·1м·10⁴Н/м³ = 1699,5кН.

2) Определение максимального выходного градиента (J_вых)_max и максимальной выходной скорости (V_вых)_max.

Т_ак’’=2·Т_ак’,

Т_ак’’=2·25,96м = 51,92м.

Т_д = 30,8м.

 Т_расч” = Т_д = 30,8м.

 ,

 ,

 ,

 ,

 .

Полный коэффициент сопротивления составляет:

ζ_f’’=∑ζ_j = 0,51+0,8+0,19+0,5+0,93=2,93.

 ,

 ,

 ,

.

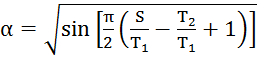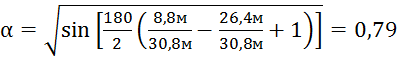(V_вых)_max = k· ,

(V_вых)_max = 1,2·10^-6м/с·0,12 = 14,4·10^-8м/с.

3) Определение удельного фильтрационного расхода q.

Т_расч”’=Т_д=30,8м. → ζ_f’”=2,93.

 ,

 .

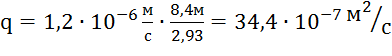Все пункты изображены на рис.1.

3. Сравнение результатов расчета

Сравнение полученных результатов методом ЭГДА и МКС для лучшего восприятия занесем в таблицу (табл.3).

Таблица 3

	ЭГДА	МКС	Расхождение, %
F, Н	1660,8·103	1699,5·103	2,3
Jвых	0,183	0,12	34,4
Vвых, м/с	21,96·10-8	14,4·10-8	34,4
q, м2/с	32,5·10-7	34,4·10-7	5,8

 .

 .

 .

 .

 .

Литература

1. Кожевникова Е.Н., Лаксберг А.И., Локтионова Е.А. Механика жидкости и газа (гидравлика). Справочник: Учеб. пособие. СПб.: Изд-во Политехн. ун-та, 2007. 90с.

2. Кожевникова Е.Н., Локтионова Е.А., Орлов В.Т. Механика жидкости и газа (гидравлика). Метод. рекомендации для выполнения и оформления курсовых и расчетно-графических работ. СПб.: Изд-во Политехн. ун-та, 2006. 39 с.