Расчёт фильтрации через земляную плотину

Санкт-Петербургский государственный политехнический университет

Инженерно-строительный факультет

Кафедра гидравлики

Расчетно-графическое задание №2

Дисциплина: Гидравлика

Тема: Расчёт фильтрации через земляную плотину

Выполнил студент группы 3013/1             Шепетько В.В.

     Преподаватель                                         Локтионова Е.А.

«_____»______________2011г.

Санкт-Петербург

2011

Содержание

1. Расчёт однородной плотины на водонепроницаемом основании …………..4

    1.1. Определение удельного фильтрационного расхода …………………. 4

    1.2. Построение кривой депрессии ……………………………….…………. 7

    1.3. Построение гидродинамической сетки ……………………….……….. 7

2. Расчет плотины с ядром …………………………………………………….. 11

    2.1. Расчет плотины с дренажным банкетом …………………………….. 11

    2.2. Расчет плотины с ядром и дренажным банкетом …………………… 13

Литература ……………………………………………………………..………. 15

1. Расчёт однородной плотины на водонепроницаемом основании

По заданию дано поперечное сечение земляной плотины, расположенной на водонепроницаемом основании. Тело плотины выполнено из однородного грунта, имеющего коэффициент фильтрации k=0,0004см/с.

1.1. Определение удельного фильтрационного расхода

Для определения удельного фильтрационного расхода необходимо заменить действительный профиль на расчетный с вертикальной входной гранью исходя из следующих условий:

- q_расч = q_действ,

- (КД)_расч ≈ (КД)_действ.

Вычислим коэффициент ε:

,

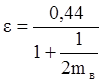где m_в – коэффициент откоса верхнего бьефа.

.

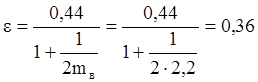Отсюда:

ε·h₁ = 0,36·12,7м = 4,572м.

Теперь разбиваем полученную модель на два фрагмента:

I – область плавноизменяющегося движения,

II – область резкоизменяющегося движения.

Вычислим для каждой области отношение удельного фильтрационного расхода на коэффициент фильтрации:

 ,

 ,

где h₁ и h₂ – уровень воды в верхнем и нижнем бьефах соответственно, м,

  m_н – коэффициент откоса нижнего бьефа.

Расстояния L определяется следующим образом::

L = ε·h₁ + b_o +(h₁ – h₂)·m_н - Δ· m_н = L_o - Δ· m_н.

L_o = ε·h₁ + b_o +(h₁ – h₂)·m_н,

L_o = 4,572м + 8,5м +(12,7м – 4м)·2,0 = 30,472м.

Полученную систему уравнений решим графическим способом. Составим табл.1, зависимость (q/k)_I и (q/k)_II от Δ.

Таблица 1

Пример расчета табл.1 для Δ=0,5м:

1) Δ=0,5м,

2) L = 30,472м – 0,5м·2,0 = 29,472м,

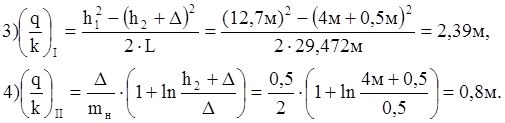
По данным табл.1 строится график зависимости q/k от Δ (рис.1). И графика видно, что Δ_иск = 2,34м и (q/k)_иск = 2,34м.

Зная (q/k)_иск можно вычислить удельный фильтрационный расход, умножив полученное отношения на k:

q = (q/k)_иск·k,

q = 2,34м·0,0004·10^-2м/с = 9,36м²/с.

1.2. Построение кривой депрессии

Определив отношение удельного фильтрационного расхода на коэффициент фильтрации можно построить кривую депрессии. Для этого воспользуемся следующей формулой:

 ,

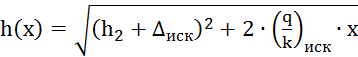где h – отметка кривой депрессии в зависимости от расстояния x.

Для построения кривой депрессии в данной работе берется десять точек, с шагом примерно L/10 (). Первые девять точек возьмем с шагом 2,5м, а последнюю через 3,292м. В качестве проверки, последнее расстояние x должно быть равно L, а последняя отметка h = h₁. Составим табл.2, зависимость отметки h от расстояния x, и полученные результаты наносим на схему плотины (рис.2).

Таблица 2

x	м	2,5	5	7,5	10	12,5	15	17,5	20	22,5	25,792
h	м	7,2	8,0	8,7	9,3	9,9	10,5	11,0	11,6	12,1	12,7

Пример расчета табл.2 для x=2,5м:

1) x=2,5м,

2) h = = 7,2м.

График кривой депрессии представлен на рис.2.

Так как действительный профиль плотины был заменен на расчетный, то после построения кривой депрессии по табл.2 необходимо откорректировать ее. То есть, кривая депрессии должна начинаться (если смотреть на рисунок слева направо) с глубины h₁ от стенки плотины под углом 90⁰. Исправления занесены на рис.2.

1.3. Построение гидродинамической сетки

Гидродинамическая сетка – это совокупность ортогонально расположенных линий тока и линий равного напора.

Для построения гидродинамической сетки подберём такие целые числа m и n, чтобы выполнялось следующее равенство:

 ,

где Н – разность уровней в верхнем и нижнем бьефах (H=h₁ – h₂), м.

.

Таким образом, m=8, n=2. Число промежуточных линий равного напора составляет (m-1)=7, а число промежуточных линий тока (n-1)=1.

Чертеж гидродинамической сетки представлен на рис.3.

2. Расчет плотины с ядром

По заданию дано поперечное сечение земляной плотины, расположенной на водонепроницаемом основании. Плотина имеет ядро, выполненное из глинистого грунта, и дренаж в виде банкета из каменной наброски.

2.1. Расчет плотины с дренажным банкетом

В данном случае считается, что потерь напора нет. И рассматриваться будет плавноизменяющееся движение (L).

Удельный фильтрационный расход вычисляется по следующей формуле:

,

где L = ε·h₁ + b_o + (h₁ – (h₂ + 1))·m_н – (h₂ + 1)·m,

L = 4,572м + 8,5м + (12,7м – (4м + 1))·2,0 – (4м + 1)·1 = 23,5м.

 .

q/k = 12,4·10^-6 / 4·10^-6 = 3,1м.

Аналогично п.1.2. строим кривую депрессии. Уравнение кривой депрессии выглядит так:

 .

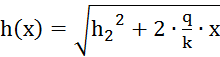Кривую депрессии строим по значениям из табл.3.

Таблица 3

x	м	2,5	5	7,5	10	12,5	15	17,5	20	22,5	23,5
h	м	5,6	6,9	7,9	8,8	9,7	10,4	11,2	11,8	12,5	12,7

Пример расчета табл.3 для x=2,5м:

1) x=2,5м,

2) h = = 5,6м.

График кривой депрессии представлен на рис.4.

2.2. Расчет плотины с ядром и дренажным банкетом

В данной задаче неоднородный грунт заменяется на однородный. То есть рассматривается виртуальная схема. Вычислим виртуальную толщину ядра:

 ,

 .

Удельный фильтрационный расход высчитывается по такой же формуле, как и п.2.1, но вместо L подставляется L_В:

 ,

L_В = L – δ_Я + δ_В.

L_В = 23,5м – 2,7м + 324м = 344,8м,

 .

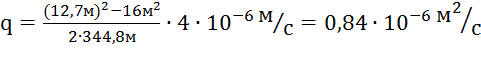q/k = (0,84м²/с) / (4м/с) = 0,21м.

Теперь можно построить кривую депрессии. Уравнение кривой депрессии выглядит следующим образом:

 .

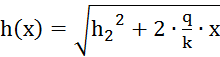Кривую депрессии строим по значениям из табл.4.

Таблица 4

x	м	2	6	10	13	175	337	339	341	344	344,8
h	м	4,1	4,3	4,5	4,6	9,5	12,55	12,58	12,62	12,68	12,7

Пример расчета табл.4 для x=2м:

1) x=2м,

2) h = = 4,1м.

График кривой депрессии представлен на рис.5.

Из рис.5 видно, что в ядре возникает потеря напора, которая составляет Δ_Я = 7,95м.

Литература

1. Кожевникова Е.Н., Лаксберг А.И., Локтионова Е.А. Механика жидкости и газа (гидравлика). Справочник: Учеб. пособие. СПб.: Изд-во Политехн. ун-та, 2007. 90с.

2. Кожевникова Е.Н., Локтионова Е.А., Орлов В.Т. Механика жидкости и газа (гидравлика). Метод. рекомендации для выполнения и оформления курсовых и расчетно-графических работ. СПб.: Изд-во Политехн. ун-та, 2006. 39 с.