Другие предметы \ Гидравлика

Определение глубины равномерного движения на отводящем участке канала. Определение средних скоростей движения воды в канале, страница 5

12.  По формуле (3.1):

 = 52,7 / 17,88 = 2,95 м/с;

13.  По формуле (6.3):

;

14.  i2 – i1уч = 0,00013–0,00233 = -0,00220;

15.  По формуле (6.4):

Δl1 = -0,03 / -0,00220 = 15,15 м.

По данным табл. 7.2 строим кривую свободной поверхности bI при условии, что глубина в конце канала равна критической глубине (рис.7.1).



8.  ПОСТРОЕНИЕ КРИВЫХ СВОБОДНОЙ ПОВЕРХНОСТИ НА ПОДВОДЯЩЕМ И ОТВОДЯЩЕМ УЧАСТКАХ КАНАЛА ПРИ ПОЛНОСТЬЮ ОТКРЫТОМ ЗАТВОРЕ.

h01’ = 3,94 м;

h02 = 2,9м;

i1 = 0,0000392 <iK = 0,003;

i2 = 0,00013 <iK = 0,003;

i1<i2

При полностью открытом затворе на отводящем участке кривая свободной поверхности будет  иметь форму типа bI. На подводящем участке имеет место равномерное движение, т.е. свободная поверхность будет совпадать с линией нормальных глубин. См. рис.8.1.



9.  ПОСТРОЕНИЕ ГРАФИКА ПРЫЖКОВОЙ ФУНКЦИИ θ(h)

Прыжковая функция зависит от глубины и имеет вид:

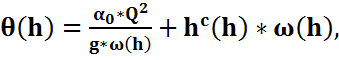(9.1)

где α0 – корректив количества движения (примем α0 = 1);

hc(h) – заглубление центра тяжести сечения, которое определяется по формуле:

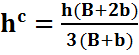.             (9.2)

Для построения графика прыжковой функции составим таблицу, в которой найдём координаты точек ей принадлежащих (табл. 9.1).

Таблица 9.1

№

h

ω

B

hc

hcω

α0Q^2/gω

Q(h)

1

0,30

3,49

12,23

0,15

0,51

81,23

81,74

2

0,50

6,02

13,03

0,24

1,46

47,12

48,58

3

0,70

8,70

13,83

0,34

2,93

32,57

35,50

4

0,90

11,55

14,63

0,43

4,95

24,54

29,50

5

1,00

13,03

15,03

0,47

6,18

21,75

27,93

6

1,10

14,55

15,43

0,52

7,56

19,47

27,03

7

1,20

16,12

15,83

0,56

9,09

17,58

26,68

8

1,22

16,43

15,91

0,57

9,42

17,25

26,66

9

1,30

17,72

16,23

0,61

10,79

15,99

26,78

10

1,40

19,36

16,63

0,65

12,64

14,64

27,28

11

1,50

21,05

17,03

0,70

14,66

13,47

28,12

12

1,70

24,53

17,83

0,78

19,21

11,55

30,77

13

1,90

28,18

18,63

0,87

24,48

10,06

34,54

14

2,00

30,06

19,03

0,91

27,39

9,43

36,82

15

2,20

33,95

19,83

1,00

33,79

8,35

42,14

Пример расчёта таблицы (для h = 0,30 м):

1.  По формуле (1.4):

ω = (11,03 + 2 * 0,30) * 0,30 = 3,49 м2;

2.  По формуле (2.1):

B = 11,03+ 2 * 2 * 0,30 = 12,23 м;

3.  По формуле (9.2):

hc = 0,30 * (12,23+ 2 * 11,03) / (3 * (12,23 + 11,03)) = 0,15м;

4.  hc * ω = 0,15 * 3,49 = 0,51 м3;

5.  α0 * Q2/ (g * ω) = 1*(52,7)2 / (9,8 * 3,49) = 81,23 м3;

6.  По формуле (9.1):

θ (h) = 81,23 + 0,51 = 81,74 м3.

По данным табл. 9.1 строим график прыжковой функции, совмещая его с графиком удельной энергии (рис. 9.1).



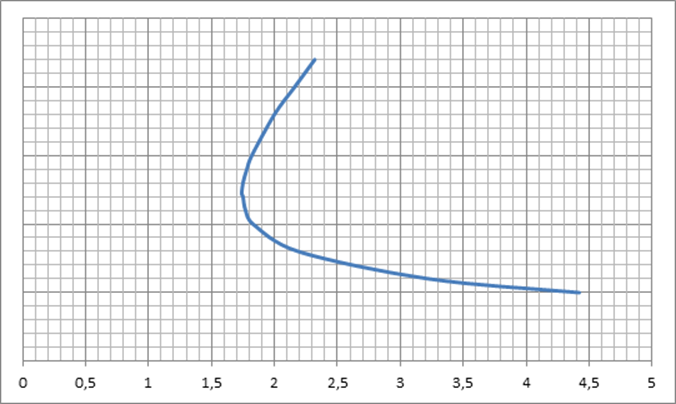
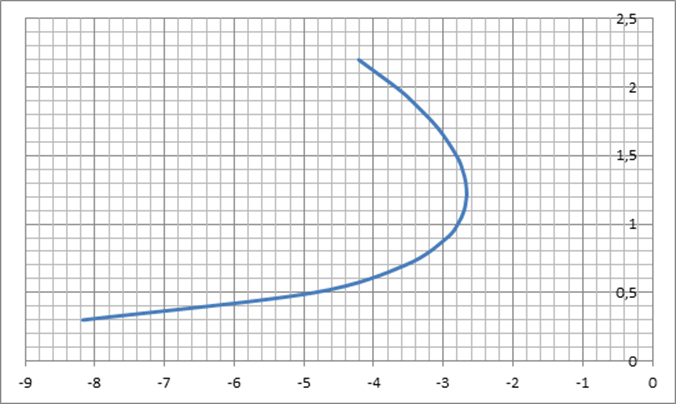Рис. 9.1. Совмещенный график удельной энергии и прыжковой функции


10. ПОСТРОЕНИЕ ЛИНИИ СОПРЯЖЁННЫХ ГЛУБИН ДЛЯ КРИВОЙ ТИПА СIИ ОПРЕДЕЛЕНИЕ МЕСТОПОЛОЖЕНИЯ  ГИДРАВЛИЧЕСКОГО ПРЫЖКА

Полагая все точки на кривой типа сI равновероятными для начала прыжка, определим по графику прыжковой функции θ(h) (рис. 9.1)соответствующие им вторые сопряжённые глубины, пользуясь свойством θ(h’) =θ(h’’).Занесём эти глубины в таблицу 10.1.

Таблица 10.1

h'

м

0,27

0,46

0,65

0,84

1,03

h''

м

3,45

2,6

2,03

1,65

1,45

По данным таблицы 10.1 построим линию вторых сопряжённых глубин (рис 7.1). Точка пересечения этой  линии с кривой типа bIсоответствует концу прыжка.

h’’действ = 1,88м.

По графику прыжковой функции обратным ходом определяем глубину в начале прыжка:

h’действ = 0,75 м.

На рис. 8.1 соединяем точки начала и конца прыжка.

11. ОПЕРЕДЕЛЕНИЕ ПАРАМЕТРОВ ГИДРАВЛИЧЕСКОГО ПРЫЖКА

Высота прыжка:

ап = h’’действ - h’действ = 1,88 – 0,75 = 1,13 м;

Длина прыжка:

lп = 6,2* h’’действ = 6,2 * 1,88 = 11,66 м;

Потеря энергии в прыжке определяется по формуле:

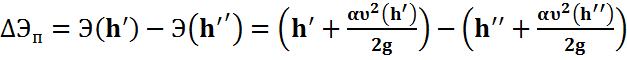. (11.1)

По формуле (1.4):

ω(h’)=(11,03 + 2 * 0,75) * 0,75 = 9,40 м;

ω(h’’)=(11,03 + 2 * 1,88) * 1,88 = 27,81 м;

По формуле (3.1):

;

.

Подставляем найденные значения скоростей в формулу (11.1):

.

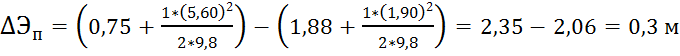Показываем это значение на графике удельной энергии сечения (рис.9.1).

На рис. 11 представлена схема гидравлического прыжка и показана напорная линия.



ЛИТЕРАТУРА

1. Механика жидкости и газа (гидравлика): Учебник для вузов / Гиргидов А.Д. СПб.: Изд-во СПбГПУ, 2002. 546 с.

2. Механика жидкости и газа (гидравлика): Метод.рекомендации для выполнения и оформления курсовых и расчетно-графических работ / Е.Н. Кожевникова, Е.А. Локтионова, В.Т. Орлов. СПб.:Изд-во СПбГПУ,2004.39 с.

3. Механика жидкости и газа (гидравлика). Справочник: Учеб.пособие / Е.Н. Кожевникова, А.И. Лаксберг, Е.А. Локтионова, М.Р. Петриченко. СПб.: Изд-во СПбГПУ, 2007. 90 с.

Скачать файл