Санкт-Петербургский государственный политехнический университет
Инженерно-строительный факультет
Кафедра гидравлики
Расчетно-графическое задание
Дисциплина: Гидравлика
Тема: Короткие трубопроводы
Выполнил студент группы 3013/1 Шепетько В.В.
Преподаватель Локтионова Е.А.
«_____»______________2010г.
Санкт-Петербург
2010
Оглавление
1. Подбор диаметра трубопровода. 4
2. Построение напорной и пьезометрической линий. 9
3. Определение максимального вакуума в сифоне. 10
4. Проверка режима движения и области сопротивления. 12
5. Определение разности уровней воды в водоемах. 13
Литература……………………………………………………………………….14
1. Подбор диаметра трубопровода
Считая, что работает только один сифон (предполагается, что второй сифон закрыт на ремонт), необходимо определить диаметр трубы сифона (сообразуясь с имеющимся сортаментом чугунных водопроводных труб). Решение задачи ведется подбором. Воспользуемся формулой расхода:
![]() , (1)
, (1)
где Q - расход жидкости в трубе, м3/с;
µт - коэффициент расхода трубопровода;
ω - площадь живого сечения трубы, м2;
Z - разность уровней в резервуаре, м.
Коэффициент расхода трубопровода можно найти по формуле:
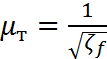 . (2)
. (2)
В формуле расхода (1) присутствуют две функции, одну из которых вычислить невозможно (µт).
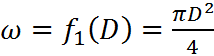 ;
; ![]() . (3)
. (3)
Необходимо преобразовать формулу (1)
и найти произведение ![]() :
:
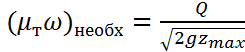 , (4)
, (4)
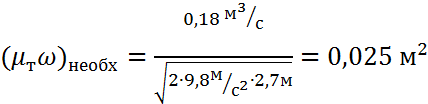 .
.
Теперь составляется таблица зависимости значений коэффициентов от диаметра трубы. При этом значение диаметра выбирается произвольно (из
табл. 4.7, стр. 41 [1]), а значения коэффициентов - исходя из формул (или таблиц из [1]) с соответствующим значением диаметра трубы D.
Табл.1. Зависимость значений коэффициентов от диаметра трубы
|
Величина |
Единица величины |
Значение величины |
||||
|
D1 |
D2 |
D3 |
D4 |
D5 |
||
|
D |
м |
0,15 |
0,25 |
0,30 |
0,35 |
0,40 |
|
ω |
м2 |
0,0180 |
0,0491 |
0,0707 |
0,0962 |
0,1256 |
|
λ |
- |
0,0191 |
0,0165 |
0,0161 |
0,0156 |
0,0151 |
|
|
- |
2,445 |
1,267 |
1,0304 |
0,856 |
0,725 |
|
ζвх |
- |
6,0 |
4,4 |
3,7 |
3,4 |
3,1 |
|
ζр.пов.450 |
- |
0,318 |
0,318 |
0,318 |
0,318 |
0,318 |
|
ζпл.пов.900 |
- |
0,101 |
0,072 |
0,069 |
0,065 |
0,062 |
|
ζвых |
- |
1 |
1 |
1 |
1 |
1 |
|
ζf |
- |
10,182 |
7,375 |
6,435 |
5,957 |
5,538 |
|
µт |
- |
0,313 |
0,368 |
0,394 |
0,409 |
0,425 |
|
µтω |
м2 |
0,006 |
0,018 |
0,028 |
0,039 |
0,053 |
Пример расчета табл.1 для диаметра трубы D=150 мм=0,15 м:
1) Вычисление площади живого сечения w:
Воспользуемся формулой (3):
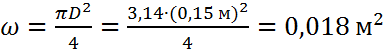 .
.
2) Установление коэффициента гидравлического трения λ:
Значение коэффициента гидравлического трения в данной работе принимается для новых битумизированных чугунных труб (из табл. 4.7 стр. 41 [1]), λср=λ=0,0191.
3) Нахождение коэффициента сопротивления по длине ζl:
![]() ,
,
где l - длина трубы сифона, м {l=4(zmax+h')=4(2,7м +2,1м)=19,2м};
![]() .
.
4) Определение коэффициента сопротивления входа ζвх:
Данная чугунная труба снабжена всасывающим клапаном с сеткой, следовательно, коэффициент сопротивления входа, зависящий от диаметра трубы, ζвх=6 (из табл. 4.16 стр. 50 [1]).
5) Установление коэффициента сопротивления резкого поворота (450) ζр.пов.450:
Из табл. 4.17 на стр.51 [1] ζр.пов.450=0,318.
6) Вычисление коэффициента сопротивления плавного поворота (900) ζпл.пов.900:
Для трубы круглого поперечного сечения коэффициент сопротивления плавного поворота находится по формуле:
![]() ,
,
где а - коэффициент, зависящий от угла поворота и определяемый по
опытным данным Кригера, а=1 (табл.4.19 стр.52 [1]),
ζ900 - коэффициент сопротивления при угле поворота 900,
определяемый по формуле:
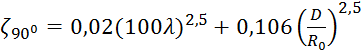 ,
,
где R0 - радиус поворота, R=1,3м (принят по заданной схеме из геометрических соображений).
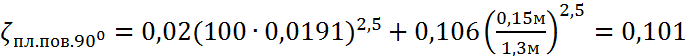 .
.
7) Установление коэффициента сопротивления выхода ζвых:
Коэффициент сопротивления выхода при любом диаметре трубы будет равен 1. (ζвых=1).
8) Вычисление полного коэффициента сопротивления ζf:
Полный коэффициент сопротивления равен сумме всех коэффициентов, то есть:
![]() ,
,
![]() .
.
9) Определение коэффициента расхода трубопровода µт:
Воспользуемся формулой (2):
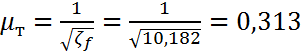 .
.
10) Нахождение произведения (µтω):
Полученные значения двух функций µт и ω {см. формулу (3)} необходимо перемножить, и это произведение (µтω) сравнивается с (µтω)необх.. Данное действие проделывается для того, чтобы понять, какие значения диаметров трубы D необходимо брать дальше.
µтω=0,313*0,018м2=0,006м2 ,
(µтω)необх.=0,025м2 {см. формулу (4)}.
Так как полученное произведение получилось намного меньше необходимого, то дальнейшее значение диаметра трубы нужно выбирать где-то в 4 раза больше.
Проведя аналогичные операции для других стандартных D, по данным табл.1 на рис.1 строим график зависимости µтω=f(D).
Найденное по графику значение Dиск.=0,29м округляем до ближайшего большего значения Dстанд. Из табл. 4.7 стр.41 [1] следует, что ближайший больший диаметр трубы составляет 300мм, следовательно, D=0,3м (µтω=0,028м2).
Теперь необходимо вычислить действительное значение разности уровней в резервуарах Zдейств:
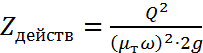 ,
,
![]() ,
,
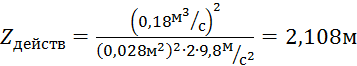 . (5)
. (5)
2. Построение напорной и пьезометрической линий
Из выше проделанных вычислений следует, что данная чугунная труба имеет диаметр D=0,3м, λ=0,0161, µтω=0,028м2.
Для построения напорной и пьезометрической линий необходимо знать следующие величины потерь напора:
1) Потери напора по длине hl:
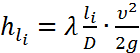 ,
,
где li - длина напорной линии на определенном участке i (i=1,...,4), м;
υ - средняя по сечению скорость напора воды, м/с.
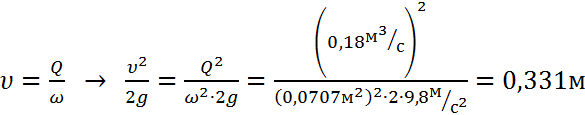 .
.
Для первого и четвертого участков (l1=l4=1,92м):
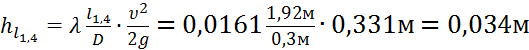 .
.
Для второго и третьего участков (l2=l3=7,68м):
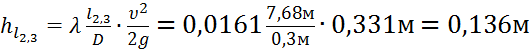 .
.
Общая потеря напора по длине:
![]() .
.
2) Местные потери напора:
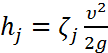 ,
,
- на входе (ζвх=3,7):
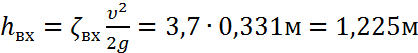 ,
,
- при резком повороте на 450 (ζр.пов.450=0,318):
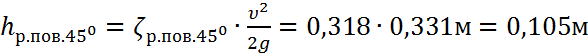 ,
,
- при плавном повороте на 900 (ζпл.пов.900=0,069):
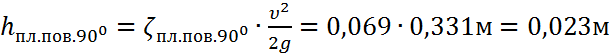 ,
,
- на выходе (ζвых=1):
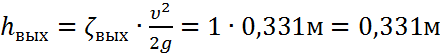 .
.
3) Вычисление общей потери напора:
Это сумма всех потерь напора:
hf=hl+hвх+2hр.пов.450+hпл.пов.900+hвых=(0,34+1,225+2*0,105+0,023+0,331)м,
hf=2,129м .
Полученное значение hf должно быть примерно равно значению Zдейств (5):
hf=2,129м ≈ Zдейств=2,108м.
По полученным результатам строится напорная линия, начиная с
водоема А. Пьезометрическая линия
строится по напорной, при этом откладывается величина ![]() , и построение начинается с водоема
В (рис.2).
, и построение начинается с водоема
В (рис.2).
3. Определение максимального вакуума в сифоне
Из рис. 2 видно, что величина вакуума в сифоне составляет 4 м водяного столба, что не превышает допустимых значений вакуума.
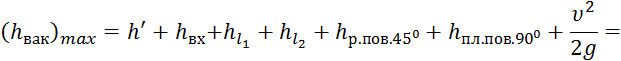
![]() ,
,
![]() ,
,
где (hвак)доп - допускаемый вакуум по условию неразрывности сплошности струи {(hвак)доп=6...7м}.
4. Проверка режима движения и области сопртивления
Критерием режима движения является число Рейнольдса, которое можно определить по следующей формуле:
![]() ,
,
где υ - средняя по сечению скорость, (υ =2,546м/с),
D - диаметр трубы, (D=0,3м),
ν - кинематический коэффициент вязкости, м2/с.
Из табл. 2.12 стр. 16 [1] кинематический коэффициент вязкости ν=1,792*10-6 м2/с при температуре воды t=00С.
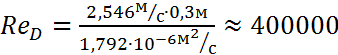 . (6)
. (6)
Так как полученный результат ReD=400000 ≥ (ReD)''кр=4000, то данный вид движения турбулентный.
Для определения области сопротивления необходимо полученное число Рейнольдса (6) сравнить с предельными числами Рейнольдса - (ReD)'пр и (ReD)''пр:
- нижнее предельное число Рейнольдса (ReD)'пр:
![]() ,
,
где ∆r - относительная шероховатость, ![]() ,
,
где ∆ -
абсолютная шероховатость (берется из справочника [1]
табл. 4.3 стр. 37 в соответствии с материалом трубы).
Для новых чугунных труб интервал значений абсолютной шероховатости составляет 0,25-1,0мм, но наиболее вероятное значение ∆=0,7мм. Следовательно,
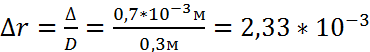 ,
,
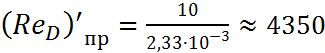 .
.
- верхнее предельное число Рейнольдса (ReD)''пр:
![]() ,
,
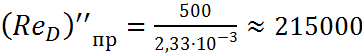 .
.
Так как полученное число Рейнольдса (ReD=400000) больше верхнего предельного числа Рейнольдса ((ReD)"пр ≈ 215000), следовательно, данная область сопротивления - область квадратичного сопротивления.
5. Определение разности уровней воды в водоемах
Нахождение разности уровней воды в водоемах A и B в предположении, что работают оба сифона, диаметры которых составляют 0,3м, производится по следующей формуле:
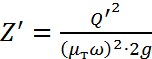 ,
,
Так как работают оба сифона, то расход воды, проходящий через один сифон, уменьшится в два раза: Q' = Q/2, следовательно:
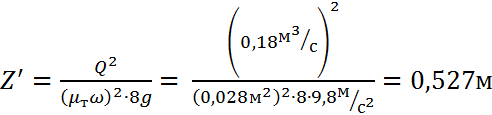 .
.
Литература
1. Кожевникова Е.Н., Лаксберг А.И., Локтионова Е.А. Механика жидкости и газа (гидравлика). Справочник: Учеб. пособие. СПб.: Изд-во Политехн. ун-та, 2007. 90с.
2. Кожевникова Е.Н., Локтионова Е.А., Орлов В.Т. Механика жидкости и газа (гидравлика). Метод. рекомендации для выполнения и оформления курсовых и расчетно-графических работ. СПб.: Изд-во Политехн. ун-та, 2006. 39 с.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.