Контрольные вопросы и задания
1. Дайте определение напряженности электростатического поля; потенциала.
2. Чему равна потенциальная энергия положительного диничного заряда в поле, создаваемом точечным зарядом?
3. Покажите, что силовые линии напряженности лектростатического поля ортогональны эквипотенциальным поверхностям.
4. Как математически связаны потенциал и напряженность поля?
5. Какое поле называется потенциальным? Является ли поле тяготения потенциальным?
6. Какие поверхности (линии) называются эквипотенциальными?
Рекомендательный библиографический список
1. Савельев И.В. Курс общей физики. Т. 2. - М., 1970. - § 6, 7, 10,12.
2. Савельев И.В. Курс общей физики. Т. 2. - М, 1978. - § 5, 6, 8.
3. Физический практикум (электричество и оптика)/ Под ред.В.И. Ивероновой. - М, 1968.- Задача 65.
4.Яворский Б.М. Курс физики. Т. 2. - М, 1966. - § 21, 23, 33.
Лабораторная работа № 3-2
БАЛЛИСТИЧЕСКИЙ ГАЛЬВАНОМЕТР И ЕГО ПРИМЕНЕНИЕ ДЛЯ ИЗМЕРЕНИЯ ЕМКОСТИ
Цель работы. Изучить баллистический метод измерения заряда на примере определения емкости конденсатора.
Приборы и принадлежности: баллистический гальванометр с осветителем и шкалой; вольтметр, выпрямитель, реостат, исследуемые и эталонные конденсаторы.
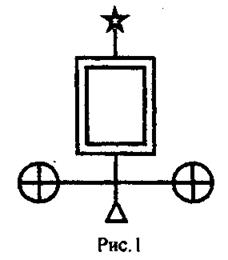Баллистический гальванометр представляет собой гальванометр магнитоэлектрической системы, у которого
искусственно увеличен момент инерции
его подвижной части. Увеличение можег быть достигнуто, например, скреплением
с подвижной рамкой стерженьков с чашечками , в которых помещено по тяжелому шарику (рис. 1).
Поскольку период собственных колебаний рамки пропорционален квадратному корню из момента инерции I,
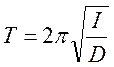(1)
где D- модуль кручения, то увеличение момента инерции приводит к возрастанию периода колебаний рамки, что существенно для рассматриваемого баллистического метода. Движение рамки в общем случае описывается неоднородным дифференциальным уравнением второго порядка, полное решение которого довольно громоздко. При измерениях баллистическим гальванометром время протекания тока τ мало и можно считать
(2)
В этом случае основные закономерности работы гальванометра можно получить более простым путем.
Вращающий момент, действующий на рамку при пропускании через нее тока, пропорционален силе тока I:
Mi=kiI (3)
Импульс момента
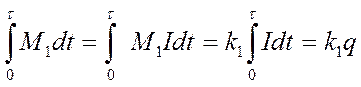(4)
где q - заряд, прошедший через рамку гальванометра за время т. По основному закону динамики вращательного движения,
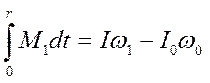(5)
где Iω-момент импульса рамки.
Поскольку рамка начинает движение из положения равновесия , то начальный момент импульса I0ω0 = 0, поэтому I1ω1=k1q.
Ввиду условия (2) можно считать, что момент t — 0. Кинетическая энергия рамки
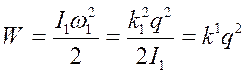(6)
где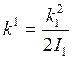 
.
Закручивание нити сопровождается появлением момента упругих сил, равного по закону Гука
(7)
При максимальном отклонении рамки на угол φ0 ее кинетическая энергия полностью перейдет в потенциальную энергию упругой деформации
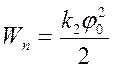(8)
Приравнивая (6) и (8), найдем, что
(9)
где β- динамическая постоянная прибора. Она определяет количество электричества, при протекании которого через рамку последняя повернется на уголэ равный одному радиану. Равенство (9) выражает основное свойство режима работы гальванометра: максимальный поворот рамки пропорционален количеству протекающего через нее электричества. Отклонение фо рамки гальванометра отсчитывается на линейной шкале по отклонению светового зайчика, расположенной на расстоянии / от рамки. Так как при повороте зеркала (и рамки) на угол ф луч поворачивается на угол 2φ , то
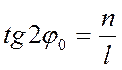(10)
где n - отсчет по шкале.
При малых углах 
, тогда
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.