б) относительная погрешность- отношение абсолютной погрешности к действительному значению измеряемой величины в процентах:
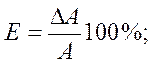
в) погрешности показаний стрелочных измерительных приборов выражаются в процентах от номинального значения (верхнего предела измерительного прибора) измеряемой величины, характеризующего прибор; в этом случае они называются приведенными относительными погрешностям, т. е.
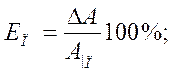 или
или 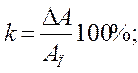 (1)
(1)
где An - предельное значение измеряемой величины (наибольшее ее значение по шкале прибора).
По ГОСТ нумеруется наибольшая приведенная погрешность, по величине которой измерительные приборы разделяются на семь классов точности; 0,1; 0,2; 0,5; 1,0; 1,5; 2,5; 4,0. Значение класса точности прибора помещается на лицевой стороне прибора внутри небольшого кружочка или без кружочка. Зная класс точности, легко определить наибольшую абсолютную погрешность. Действительно, согласно формуле (1)
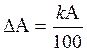 (2)
(2)
Класс точности - это абсолютнаяошибка прибора в процентах номинального значения измеряемой величины. Так как абсолютная погрешность (определяется выражением (2)) остается постоянной по всей шкале, то относительная погрешность будет тем больше, чем меньше значение измеряемой величины.
В электрических измерениях в качестве эталонов часто применяются магазины сопротивлений, емкостей, индукгивностей. Для таких приборов класс точности указывает на возможное отклонение от набранного значения, выраженное в процентах.
Для магазинов класс точности равен их относительной ошибке, которая одинакова для любого набранного значения.
Графическое представление результатов
Зависимость одной физической величины от другой, например у=f(x), может изображаться графически. Для построения пользуются в большинстве случаев прямоугольной системой координат.
На миллиметровой бумаге откладывают по оси абсцисс в произвольно выбранном масштабе значения одной из величин, а по оси ординат -значения другой величины, и полученные на плоскости точки соединяют непрерывной плавной кривой, проходящей через доверительный интервал; если плавная кривая не получается, в наблюдениях допущены ошибки.
Пользуясь кривой, можно в пределах проведенных наблюдений интерполировать, т. е, находить значения величины у для таких значений х, которые не измерялись. Из точки оси абсцисс проводят ординату до пересечения с кривой; длина ординаты представляет значение у для соответствующего значения величины х. На рис. I приведен пример построения кривой по экспериментальным точкам. Численные значения результатов измерений определяются доверительным интервалом или приборными ошибками. В данном примере величина х измерялась точнее, чем величина^, поэтому экспериментальные точки приняли вид штрихов.
Кроме системы координат с равномерным масштабом применяют полулогарифмические и логарифмические шкалы. Полулогарифмическая система координат (рис.2) удобна для построения кривых вида
![]()
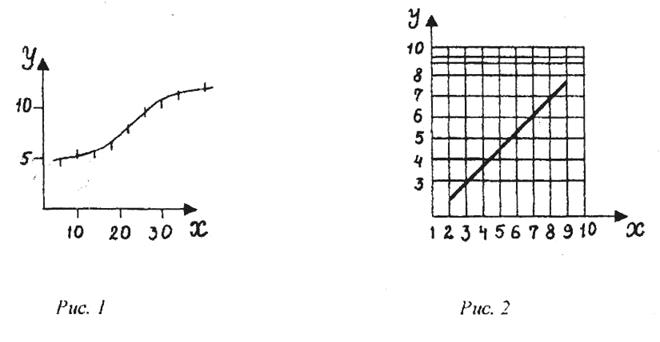 |
Если значение х откладывать по оси абсцисс (равномерная шкала), а значения у по оси ординат (логарифмическая шкала), то график даст прямую линию.
Правила при работе в лаборатории электрических и магнитных измерений
1. При сборке схемы необходимо следить за тем, чтобы включаемые измерительные приборы, реостаты и аппараты соответствовали рабочим значениям токов и напряжений.
2. Сборку сложных схем следует начинать с основной последовательной цепи, а затем уже подключать параллельные цепи.
3. Собранную схему должен проверить преподаватель. После разрешения преподавателя можно включить схему под напряжение.
4. Всякие пересоединения в схеме должны выполняться при выключен ных источниках. После каждого пересоединения схема проверяется преподавателем.
5. По окончании работы каждый студент должен получить у преподавателя пометку, что результаты работы верны. Только после этого можно приступить к разборке схемы, отключив предварительно питание.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.