Если затухание в контуре невелико (b <<wо ), то
![]() l=pRÖ(C/L) . (10)
l=pRÖ(C/L) . (10)
Как видно из (10), логарифмический декремент затухания зависит от параметров контура R, L, C и является характеристикой контура.
Качество, избирательность колебательного контура обычно характеризуются его добротностью - величиной, обратно пропорциональной логарифмическому декременту затухания Q=n/l. При малом затухании
![]() Q=wo/(2/3) = (ÖL/C )/R (11)
Q=wo/(2/3) = (ÖL/C )/R (11)
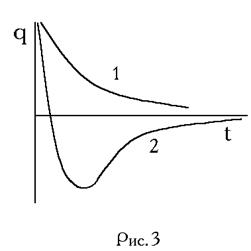 Процесс, протекающий в контуре, утрачивает свою
периодичность, когда wо<b. В этом случае подкоренное выражение (6) становится отрицательным.
Такой процесс называется апериодическим. Он характеризуется большим
затуханием, когда система, выведенная из состояния равновесия, приходит
в исходное состояние, не совершая колебаний, либо переходит через положение
равновесия, но при обратном ходе постепенно возвращается к нему (рис.3),
кривые 1 и 2 соответственно).
Процесс, протекающий в контуре, утрачивает свою
периодичность, когда wо<b. В этом случае подкоренное выражение (6) становится отрицательным.
Такой процесс называется апериодическим. Он характеризуется большим
затуханием, когда система, выведенная из состояния равновесия, приходит
в исходное состояние, не совершая колебаний, либо переходит через положение
равновесия, но при обратном ходе постепенно возвращается к нему (рис.3),
кривые 1 и 2 соответственно).
Увеличивая активное сопротивление R, можно переводить квазипериодический процесс колебаний в контуре в апериодический. Критическое сопротивление, выше которого процесс апериодический, можно найти из равенства нулю подкоренного выражения (6). В этом случае wо = b и
Rkp = 2Ö(L/C). (12)
Если включить в колебательные контур, изображённый на рис. 1, между точками 1-1 ге- нератор с переменной э.д.с. e=eо cosWt, то в контуре возникает колебание, являющееся суммой его собственных колебаний с частотой w и вынужденных - с частотой W. Через некоторое время собственные колебания в контуре затухнут и останутся только вынужденные.
В соответствии со вторым законом Кирхгофа
UR+UC=esi+e. (13)
Уравнение (4) в этом случае будет иметь вид
q+2bq+woq=(1/L)eocosWt. (14)
Решением этого уравнения будет
q=qmcos(Wt-j). (15)
Величину тока при установившихся вынужденных колебаниях найдём дифференцированием выражения (15). Амплитуда тока Im и его начальная фаза j определяются как:
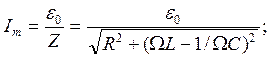
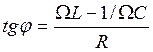 (16)
(16)
где Z - полное сопротивление контура; WL =XL - индуктивное сопротивление контура; 1/(WC) = XC - ёмкостное сопротивление; XL-XC=X - реактивное сопротивление контура.
Проанализируем выражения (16) при изменении частоты вынужденных колебаний W. Если W®0, то 1/(WC)®¥. При этом полное сопротивление контура обращается в бесконечность, а Im=0.
С увеличением W квадрат реактивного сопротивления X = (WL-1/Wc) сначала уменьшается. Поэтому полное сопротивление Z уменьшается, а Im - увеличивается.
При частоте W=wо выполняется условие WL = 1/(WC), следовательно, реактивное сопротивление обращается в нуль, а полное становится наименьшим, равным активному сопротивлению контура, т.е. контур действует как чисто активное сопротивление:
Zmin=R.
Величина тока при этом достигает максимума.
Этот случай вынужденных колебаний называется резонансом напряжений, так как колебания напряжения на конденсаторе и на индуктивности имеют одинаковые амплитуды, но разность фаз междуними равна p, т.е. их сумма равна нулю. Остаются колебания напряже-ния на активном сопротивлении.
При W>wo квадрат реактивного сопротивления X возрастает, и в соответствии с этим полное сопротивление Z увеличивается, а амплитуда тока Im уменьшается, асимптотически приближаясь к нулю при стремлении W к ¥.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.