Дифференциальный метод. Метод замещения. Косвенный метод. Меры электрических величин, страница 10

Цель работы. Освоить методы измерения электрического сопротивления металла, определить удельное сопротивление, оценить среднюю длину свободного пробега и среднюю скорость направленного- движения электронов проводимости.

Приборы и принадлежности: Прибор FPM-01 для измерения удельного сопротивления, содержащий источник регулируемого постоянного напряжения, миллиамперметр с внутренним сопротивлением R_A=0,15 Ом, вольтметр с внутренним сопротивлением Rv= 2500 Ом, Прибор оснащен стойкой, к неподвижным кронштейнам которой крепится резистивный провод из хромоникелевого сплава (78 % Ni; 22 % Сг). Между кронштейнами расположено подвижное электрическое контактное устройство, с помощью которого можно изменить длину рабочего участка провода; для измерения диаметра провода применяется микрометр.

Теоретическое обоснование

Электропроводность металлов обусловлена тем, что в металлах содержится       огромное       количество         носителей тока - электронов проводимости, образовавшихся из валентных электронов атомов металла Электроны проводимости не принадлежат определенному атому, а являются коллективизированными (обобществленными) электронами.

В классической электронной теории электропроводности металлов эти электроны рассматриваются как электронный газ. При этом пренебрегают взаимодействием электронов между собой, считая, что они соударяются лишь с ионами, образующими кристаллическую решетку. В промежутках между соударениями электроны движутся свободно, пробегая в среднем путь <>. Средняя арифметическая скорость электронов определяется аналогично средней арифметической скорости теплового движения молекул идеального газа:

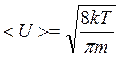                                                 (1)

где т - масса электрона; Т -температура; к = 1,38-10²³ Дж/К (постоянная Больцмана).

Число  электронов проводимости   в единице        объема одновалентногометалла может быть определено по формуле

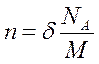                                                                                                           (2)

где - плотность металла;   N_л =6,02-10²³моль^-1   (постоянная Авогадро); М - молекулярная масса металла.

Электрический ток I возникает при наличии электрического поля внутри металла, которое вызывает упорядоченное движение электронов с некоторой средней скоростью < >. Ток можно охарактеризовать с помощью вектора плотности тока j , который численно равен электрическому заряду, проходящему за единицу времени через единичную площадку, перпендикулярную направлению упорядоченного движения заряженных частиц:

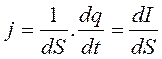
При равномерном распределении плотности электрического тока jпо сечению проводника  S

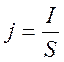
Плотность тока связана с концентрацией электронов п, зарядом электрона е и скоростью направленного движения <и> соотношением

          .                                                (4)

На основании классических представлений формула (4) может быть преобразована в формулу

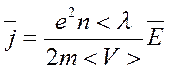.                                           (5)

Из  (5)  видно,  что плотность  тока     пропорциональна напряженности электрического поля Е и соотношение (5) выражает закон Ома в дифференциальной форме

                                                                                                                                            (6)

     ^где                                                             

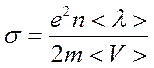                                                                                ⁽⁷⁾  

удельная электропроводность металла. Величина

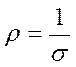                                                       (8)

называется  удельным   сопротивлением   материала.   Тогда  (6) можно записать в виде

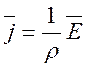
Если бы электроны не сталкивались с ионами решетки, длина свободного пробега <> и, следовательно, проводимость  были бы очень большими, а удельное сопротивление р пренебрежимо малым. Таким образом, согласно классическим представлениям, электрическое сопротивление металлов обусловлено соударениями электронов проводимости с ионами кристаллической решетки. Несмотря на весьма приближенные допущения, классическая электронная теория качественно объясняет многие законы постоянного тока. Экспериментально удельное сопротивление  металла может быть получено при измерении сопротивления Rобразцов исследуемого материала: