Учет сдвига фаз между током и напряжением удобно производить рассматривая переменный ток, напряжение и сопротивление как комплексные величины
Комплексные величины могут геометрически отображаться в виде векторной диаграммы, на которой по оси х откладывается действительная часть, а по оси у – мнимая часть комплексного выражения, тогда модуль комплексного выражения р выражается по правилу Пифагора.
![]()
Для участков цепи с последовательным соединениями ток во всех элементах одинаков и ось х называется осью тока, а ось у – осью напряжения. Поэтому полное сопротивление в электрической цепи, содержащей последовательное соединение индуктивности, електроемкости и активного сопротивления определяется в виде:
![]()
Описание установки и принцип её работы
 Мостовой метод позволяет осуществить наиболее
точные измерения электрических сопротивлений. Рассмотрим принцип
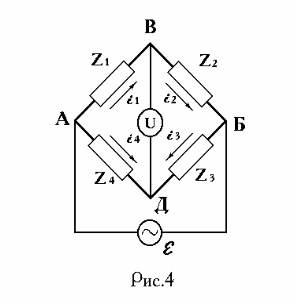
действия четырёхплечного моста . Принципиальная схема моста переменного
тока представлена на рис.4 . Здесь z1, z
2,
z 3, z 4 -
импедансы цепи . В диагональ моста ВД включён индикатор . К узлам
А и Б подаётся переменное напряжение от источника тока .
Условие равновесия любого моста переменного тока достигается тогда ,
когда потенциалы точек В и Д равны между собой в любой момент
времени , т.е. совпадают по фазе и амплитуде . Это условие выполняется
, если напряжение на полных сопротивлениях z1 и z2 равны
между собой . На основании закона Ома мы можем найти величины
токов, протекающих через эти участки электрической цепи :
Мостовой метод позволяет осуществить наиболее
точные измерения электрических сопротивлений. Рассмотрим принцип
действия четырёхплечного моста . Принципиальная схема моста переменного
тока представлена на рис.4 . Здесь z1, z
2,
z 3, z 4 -
импедансы цепи . В диагональ моста ВД включён индикатор . К узлам
А и Б подаётся переменное напряжение от источника тока .
Условие равновесия любого моста переменного тока достигается тогда ,
когда потенциалы точек В и Д равны между собой в любой момент
времени , т.е. совпадают по фазе и амплитуде . Это условие выполняется
, если напряжение на полных сопротивлениях z1 и z2 равны
между собой . На основании закона Ома мы можем найти величины
токов, протекающих через эти участки электрической цепи :
i1=e/(z1+z2) ; i2=e/(z3+z4).
Падение напряжения на сопротивлении z1 u1=i1z1, а на сопротивлении z4
u2 = i2z4 = ez4/(z3+z4).
В случае равновесия моста , т.е. u1=u2 , имеем
z1 z3 = z2 z4. (3)
Выражение (7) есть общее условие равновесие моста переменного тока в комплексной форме .
Так как zk = xk + jyk (где k = 1,2,3,4) , подставляя вместо сопротивлений zk их значения , выраженные через xk и yk ,
(x1+jy1)(x3+jy3)=(x2+jy2)(x4+jy4) (4)
Разложив на слагаемые и приравнивая отдельно действительные и мнимые части, получим
x1x3 - y1y3 = x2x4 - y2y4 ; (5)
x1y3 + x3y1 = x2y4 + x4y2 .
Только при выполнении обоих этих условий мост будет находиться в равновесии.
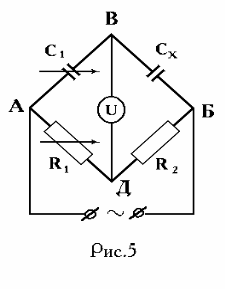 Рассмотрим схему моста для измерения ёмкости
конденсатора (мост Сотти ) , работающую на переменномтоке ( рис.2 ) .
Рассмотрим схему моста для измерения ёмкости
конденсатора (мост Сотти ) , работающую на переменномтоке ( рис.2 ) .
Процесс измерения заключается, в том что, меняя сопротивления двух других плеч R1 и R2, доби-ваются такого положения, чтобы между точками В и Д колебания напряжения были равны нулю( равновесие моста ), т.е. на экране осциллографа наблюдается прямая линия. Найдём условие равновесия моста.
В случае переменного тока нужно пользоваться комплексными сопротивлениями , т.е.
x1=0; y1=-1/(wc1);
x2=0; y2=-1/(wcx);
x3=R2; y3=0;
x4=R1; y4=0.
Поэтому условие равновесия моста на переменном токе из (9) есть
Сx / С1 = R1/R2 (6)
Измеряя соотношения R1 /R2 , необходимые для равновесия моста и зная ёмкость конденсатора C1, можно определить неизвестную ёмкость другого конденсатора Cx=C1R1/R2 .
1. Собрать электрическую схему (рис. 5) . В качестве эталонного конденсатора С1 использовать магазин ёмкостей Р513 , а в качестве R1 и R 2 - магазины сопротивлений типа Р33 . Индикатором “и” служитосциллограф С1-67. Для источника переменного тока использовать лабораторный щиток, с клем которого снимается переменное напряжение 5-10 В. с частотой 1000 или 50 Гц.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.