Дифференциальный метод. Метод замещения. Косвенный метод. Меры электрических величин, страница 15

КОЛЕБАНИЙ  В  ЭЛЕКТРИЧЕСКОМ  КОНТУРЕ

Цель работы:  изучение  затухающих  колебаний  и  условий возникновения   резонанса   напряжений  в  колебательном   контуре,  определение параметров колебательного контура.

Приборы   и   материалы:    звуковой    генератор,    вольтметр    переменного тока,  электронный  осциллограф,  кассета  с  катушками  индуктивности,  конденсаторами,  резисторами;  в  комплексе   “Каскад”  -кассеты ФПЭ-10,  ПИ/ФПЭ-09,  магазин  сопротивлений.

Общие положения

Электрическая цепь,  содержащая  индуктивность  L, конденсатор С и сопротивление  R,   в   которой  могут  возбуждаться  электрические  колебания,  называется  колебательным  контуром.  Если   конденсатор   зарядить  до   напряжения  Uo,  сообщив  заряд  qo,  контур  получит  запас энергии   WE = Cuo/2 = qo/2C.   Так   как   конденсатор   замкнут    на    индуктивность,   в   контуре  потечёт   электрический   ток,    ограниченный э.д.с.   самоиндукции.   Ток   достигнет  максимального  значения  в  момент    времени,     соответствующий  переходу  энергии   электрического поля  ( полному переходу при R=0 ) в энергию  магнитного поля   индуктивности   WH=LI /2.

В  отсутствие  потерь  ( при R=0 )  в  идеальном   контуре   возникают свободные гармонические колебания  напряжения и тока  с  собственной частотой   wо=2p/То,  где   То - период  собственных   колебаний,  равный

To=2pÖLC . Напряжение на обкладках конденсатора   меняется   во    времени  t  по   закону     U=Uocoswot,   ток    в   индуктивности      I=Iosinwot.

В  реальном  колебательном  контуре  ( R¹0 )  часть  энергии    теряется, переходит в  теплоту,  что  приводит  к  затуханию  колебаний.   Затухание   нарушает   периодичность   колебаний,   поэтому  к   ним,  строго говоря, неприменимо понятие периода и частоты.  Однако,  если  затухание мало, допустимо использование  этих  понятий,  а  процесс  в  контуре будет называться  квазипериодическим.

Для  контура,  показанного  на  рис.1,  второе  правило  Кирхгофа  запишется  в  виде

UR+UC=esi ,                                                    (1)

где   UR = RI  -  падение  напряжения  на  сопротивлении;   UC = q/C  -  напряжение    на    электрической    ёмкости;   esi  =  -L(dI/dt)  -  э.д.с.   само     индукции   индуктивности. Так  как  I = dq/dt = q, уравнение (1) запишем  в  виде         Rq + q/C = -Lq                      (2) Сделаем    перестановку     и    разделим         уравнение  (2)  на  L:             q + (R/L)q + (1/LC)q = 0          (3)

Приняв  во  внимание,  что  1/(LC) = wo   и  введя  обозначение b=R/(2L), уравнению (3)  можно придать  вид

q + 2bq +woq=0,                                              (4)

где  b  -  называется   коэффициентом   затухания.   Однородное   дифференциальное   уравнение  второго порядка (4) имеет решение

q=qoe   cos(wt + a),                                            (5)

где w - частота затухающих колебаний, равная

 

                 w=Öw0 - b    = Ö1/LC - R /4L  .                                               (6)

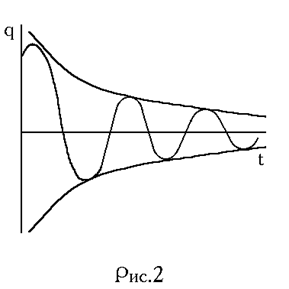
График  функции  (5)  изображён  на   рис.2.  Уменьшение  амплитуды происходит по  экспоненциальному закону

qm=qoe     .

Разделив функцию (5) на ёмкость С, получим закон изменения напряжения на конденсаторе

      U=Umcos(wt+d),                                        (7)

где   Um=Uoe    .

Чтобы  найти  величину  тока  в  индуктивности,  продифференцируем (5) по времени, и после некоторых преобразований получим

    I=Ioe     cos(wt+a-y),                        (8)      

где   p/2<y<p,   следовательно,   ток   в   индуктивности    опережает   по фазе напряжение  на  конденсаторе на угол y.

Затухание  колебаний  обычно  характеризуется логарифмическим  декрементом  затухания

l=ln[Um/Um(t+T)] = bT,                   (9)

где   Um (t +T) - амплитудное    значение    напряжения   на   конденсаторе через  период T=2p/w   от  значения  t.