Дифференциальный метод. Метод замещения. Косвенный метод. Меры электрических величин, страница 23

Общие  положения

1.   Метод  тангенс-гальванометра.

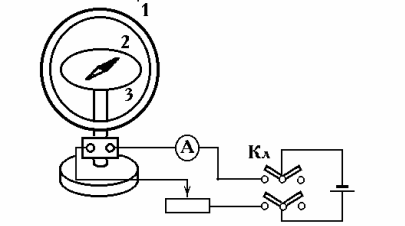
Простейшим  устройством  для  измерения  напряжённости  магнитного  поля  Земли  служит  тангенс - гальванометр, состоящий из нескольких  витков   кругового   проводника 1, в центре  которого  расположена  магнитная стрелка 2 и  угломерная шкала 3 (рис.2).   Стрелка   может    поворачиваться вокруг     вертикальной    оси.  При      отсутствии тока  в  витках  тангенс - гальванометра стрелка  располагается  в  плоскости магнитного меридиана. Пропустим постоянный   ток   I  по виткам тангенс - гальванометра.

Магнитное   поле    тока    в   центре    витков     будет    характеризоваться  вектором  напряжённости 

HВ = (I/2r)N,              (2)                                 

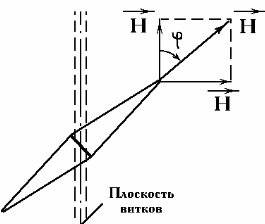который  направлен  перпендикулярно  плоскости  витков. В(1) r - радиус витков, N - число  витков. В  этом  случае  магнитная  стрелка  NS  расположится  по  направлению  результирующих  сил,  действующих  на  неё  со  стороны  магнитного  поля  рамки  и  магнитного  поля  Земли. Как  видно из  рис. 3, угол j,  который  стрелка составит с плоскостью    витков, определяется      соотношением

tgj=HB/Ho                        (3)

Подставляя в (2) вместо  НВ его  значение    из     (1),    получим

Нo =IN/2rtgj = UN/Rdtgj,             (4)

где    ток   I=U/R;    U-  напряжение  на   витках,        R -сопротивление      витков, 

r  -  радиус витков, d - диаметр  витков  (d=2r),  N- число  витков.

Измеряем  силу  тока  I или  напряжение  на  витках  U,  радиус  витков  r  угол  отклонения  стрелки  j  от  плоскости  витков  и  зная  число  витков N,  можно  определить  горизонтальную  составляющую  напряжённости  магнитного  поля  Земли.

Исходя  из  соотношений  (1)  можно  определить  вертикальную  Нz  и  полную  H  напряжённость  магнитного  поля  Земли,  принимая  для  нашей  местности  угол  наклонения  J равным  69°.

2.   Метод флюксметра

Флюксметр  состоит  из  небольшой  плоской  проволочной  катушки  (рамки),  соединённой  с  баллистическим  гальванометром.  Магнитная  индукция  В  вместе  расположения  рамки  равна

B=mmоН,                                                  (5)

а  поток  магнитной  индукции  Ф = BSNcosa  через  N  витков  измеритель- ной  рамки (m - относительная  магнитная проницаемость, в воздухе  m=1). Угол  a  находится между вектором  индукции  В и  нормалью n к  плоскости  рамки, S - площадь данного  витка.  При  повороте рамки  в  магнитном  поле  в  ней  возникает  э.д.с.  индукции

ei=-(dФ/dt)                                                (6)

и  потечёт  ток  I,  мгновенное  значение  которого  равно

I=dФ/(Rp+Rr)dt,                                           (7)

где  Rr - омическое  сопротивление  гальванометра;  Rp - сопротивление  измерительной  рамки.  Величина  тока  I  будет  изменяться, и вследствие  этого  в  электрической  цепи  на  индуктивности  L  возникнет  э.д.с. самоиндукции  es. Запишем  2-й  закон  Кирхгофа  для  замкнутого  контура:

-dФ/dt - Ldi/dt = (Rp + Rr )I.                                         (8)

Проинтегрируем  выражение  (8)  по  времени  от  момента,  когда нормаль  n  совпадает  с направлением  горизонтальной  составляющей  век- тора  индукции Во магнитного  поля  Земли  ( t=0 ),  до  момента,  когда  нормаль   перпендикулярна к Во (t=tm):

               -òdФdt/dt  -  òLdIdt/dt  =  (Rp+Rr) òIdt                                 (9)

За  время  tm  сила  тока  в  цепи изменится от  нуля  через  некоторое  максимальное  значение  Im до  нуля.  Проекции горизонтальной  состав-ляющей индукции магнитного  поля  на  нормаль  n  за  это  время  изменит- ся  от  Во до  нуля,  а  поток  через  рамку  от  Фо до  нуля.  С  учётом  ска- занного,  формулу  (9)  можно  записать  в  следующем  виде:

                   -òdФ  -  òLdI  = (Rp+Rr ) òIdt                                      (10)

Учитывая,  что  òIdt = q  есть  количество  электричества,  прошедшее  через  гальванометр  за  время  tm , и  делая  незначительные  преобразования,  получим

Bo=(Rp+Rr)q/NS                                          (11)

Количество  электричества  q  можно  определить,  измерив  отклонение  no  “зайчика”  по  шкале  гальванометра  и  зная  баллистическую  постоян-ную  гальванометра  b = q/n (см. лабораторную  работу № 3.5 [5]). Тогда  горизонтальная  составляющая  индукции  магнитного  поля  Земли  будет