В экспериментальной части была разработана программа анализа сигналов по критерию отношения правдоподобия, построенного с использованием вейвлет-спектров, и получены зависимости вероятности ошибки от отношения сигнал/шум для разных базисов, разных уровней порога значимости спектральных составляющих и разных длин сигнала. Текст программы — на приложенной дискете.
В качестве тестовых использовались две группы по 150 выборок, представляющих собой дискретизированные отсчеты сигнала от радара с высокой разрешающей способностью. Эти группы соответствуют двум разным летательным аппаратам. Рисунки, если не указано другого, приведены для 32-отсчетного преобразования.
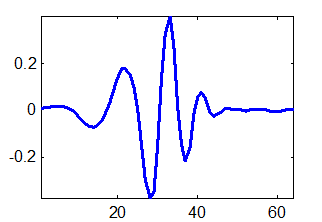
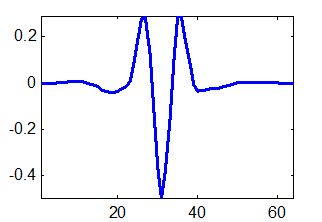
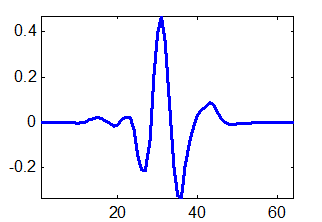
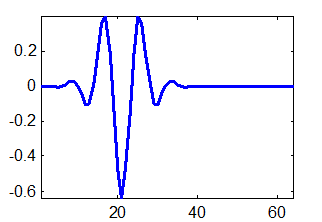
Для выполнения вейвлет-преобразования необходимо сконструировать пары фильтров декомпозиции (ВЧ — “g” и НЧ — “h”) в соответствии с методикой, изложенной в п.3.1. Эти операции включены в стандартный набор функций пакета MatLab® версии 5.2 фирмы The Mathworks, Inc., с помощью которого, в частности, были преобразованы в представленные ниже графики результаты работы программы. Поэтому для получения пар фильтров использовался этот программный продукт. Были выбраны: 15 фильтров семейства Добеши (Daubechies wavelets), 5 фильтров семейства койфлетов (coiflets), 7 фильтров семейства симлетов (symlets) и 14 фильтров семейства биортогональных вейвлетов (biorthogonal wavelets). Хотя аналитического выражения у функций, соответствующих этим фильтрам, нет, внешний вид характерных представителей функций каждого типа показан на рис. 9.1. Полный набор графиков анализирующих функций и методика их получения приведены в приложении 1.
Здесь надо заметить, что для семейств Добеши, койфлетов и
симлетов ВЧ и НЧ фильтры декомпозиции связаны формулой 
,
где L — длина фильтра, n — порядковый номер коэффициента фильтра. Фильтры реконструкции могут быть получены из фильтров
декомпозиции путем простого обращения порядка следования коэффициентов. Для
биортогональных вейвлетов эти зависимости несколько более сложны. Кроме того,
биортогональные фильтры не обеспечивают той точности восстановления сигнала,
как остальные. При этом, однако, разложение с использованием биортогональных
вейвлетов дает больше нулевых коэффициентов в результате, чем какое-либо
другое, то есть происходит обмен точности восстановления на эффективность
представления сигнала.
а) б)
в) г)
Рис. 9.1. Графики анализирующих функций: а) Добеши-6, б) койфлет-3, в) симлет-5, г) биортогональный-2.8
Как видно из рис. 9.2 и 9.3, исходно разные выборки в пределах одной группы имели различную энергию. Это повлияло бы на величину значений спектральных составляющих, поэтому выборки были подвергнуты инвариантному преобразованию с целью устранения такой зависимости. Преобразование описывается выражением
|
|
(9.1) |
то есть каждый j-тый отсчет i-той выборки был отнесен к корню из энергии этой выборки.
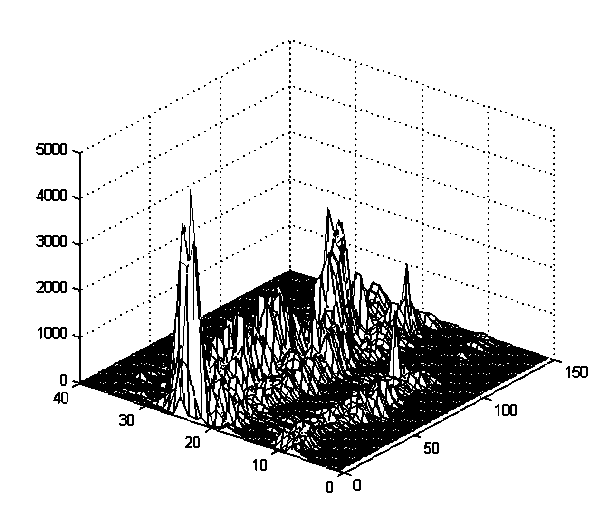
Рис. 9.2. Множество выборок первой группы
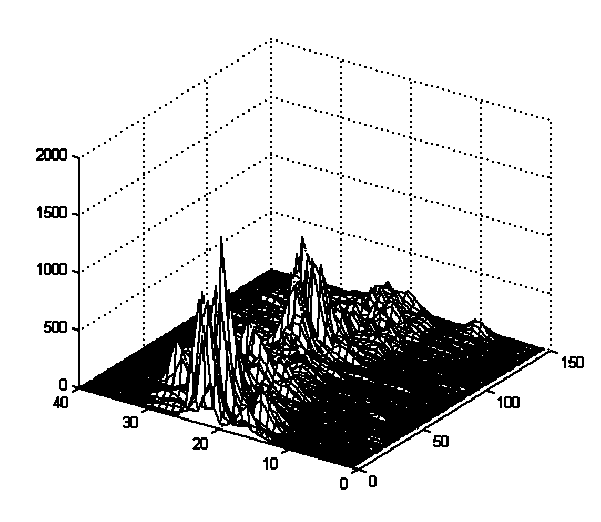
Рис. 9.3. Множество выборок второй группы
Для работы алгоритма распознавания требуется провети его «обучение» в условиях отсуствия шума. Первой задачей является поиск сигнала в стробе дальности, поскольку хотя полезный сигнал и появляется в стробе с вероятностью, равной 1, однако в случайный момент времени. В программе реализован механизм поиска полустробами.
Суть метода состоит в следующем: приходящий сигнал записывается в последовательные ячейки памяти, причем их количество равно длине ожидаемого полезного сигнала. Подсчитывается энергия в первой и второй половине ячеек (правом и левом полустробе). В случае равенства энергий считается, что полезный сигнал полностью содержится в ячейках, и их содержимое подвергается дальнейшей обработке уже как полезный сигнал. Если энергии не равны, то происходит копирование информации из старшей ячейки в младшую, начиная с самых младших, и затем в самую старшую записывается очередной отсчет. Таким образом, ячейки представляют собой своего рода «окно», которое скользит вдоль строба и фиксируется в момент равенства энергий.
Математически положение равенства описывается выражением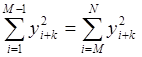 
, где N — длина полезного сигнала, M=N/2 — длина полустроба, 
—
значение i-того отсчета сигнала, k — сдвиг относительно начала
строба дальности. Ситуация иллюстрируется рис. 9.4.
Суммарная длина полустробов поиска должна равняться длине полезного сигнала. Однако исходно выборки имели разную длину (30 и 40 отсчетов). Кроме того, вейвлет-преобразование накладывает на сигнал условие, согласно которому его длительность должна быть равна сепени числа 2. В таком случае возможны были два варианта — приравнять длительность к 32 или 64 отсчетам. Первый способ вел к потере части информации о выборках второго типа, что в итоге снижало бы помехоустойчивость; второй способ давал увеличение длительности обрабатываемого сигнала без увеличения полезной информации, что также могло сказаться на помехоустойчивости. Поэтому решено было опробовать оба варианта. В таком случае длина полустробов поиска выбиралась равной 16 либо 32 отсчетам.
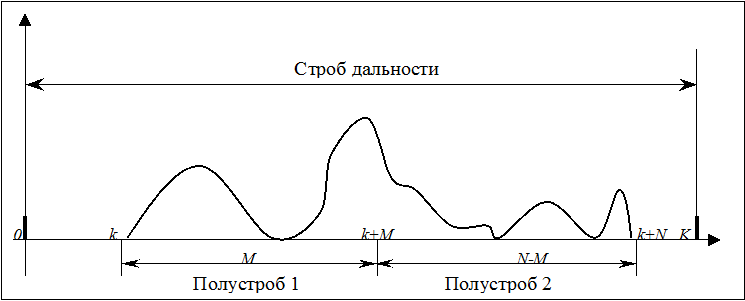
Рис. 9.4. Метод поиска сигнала полустробами
Необходимо было также учесть, что фактически энергия сигналов, которые планировалось обрабатывать, распределена во времени крайне неравномерно (см. рис. 9.2 и 9.3). Для большинства выборок основная часть энергии содержалась в отсчетах, лежащих ближе к концу выборки. Поэтому постоянно возникали бы ситуации, когда равенству энергий соответствовала не середина выборки, а некоторое сдвинутое положение. При обработке это приводило бы к потере части информации (нескольких первых отсчетов, соответствующих полезному сигналу) и захвату отсчетов, содержащих только шум (за концом полезного сигнала). Поэтому, хотя поиск проводился равными полустробами, при копировании найденного сигнала для дальнейшей обработки их длина выбиралась неодинаковой.
Исследование показало, что для 32-отсчетного преобразования лучшими длинами полустробов копирования, сохраняющими в среднем максимум полезной информации о сигнале, является 22 для левого и 10 для правого полустроба, то есть изменение длины полустробов поиска на +6(–6) для обеих групп сигналов. При этом у выборок второй группы (40-отсчетных) терялись первые 8 отсчетов, но, поскольку они содержали не более 0,2% энергии сигнала, такой потерей можно было пренебречь. Аналогичные результаты были получены для 64-отсчетных выборок. Здесь оптимальные длины полустробов копирования составили соответственно 38 и 26.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
, где 
,