Разработка программы анализа сигналов по критерию отношения правдоподобия, построенного с использованием вейвлет-спектров, страница 2

Применение отношения правдоподобия требует знания статистических характеристик спектров. Для обеих групп после нахождения синала над ним выполнялось вейвлет-преобразования в различных базисах ибыстрое преобразование Фурье [7]. Для исследования вместо полного спектра Фурье была использована его первая половина (поскольку спектр симметричен относительно центра) и реальные и мнимые составляющие рассматривались как независимые коэффициенты. Были получены следующие статистические характеристики:

·  Оценки матожиданий спектральных составляющих

,

(9.2)

где  (рис. 9.5).

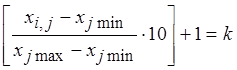Были определены данные для построения гистограмм, показывающих характер распределения отсчетов. Для каждого коэффициента были найдены минимальное  и максимальное в пределах группы значения, и 10 интервалов гистограммы были заполнены по правилу , если , где  — k-тый интервал гистограммы распределения j-того коэффициента, “” — операция взятия целой части, . На рис. 9.6(а-г) показаны гистограммы, где по оси Х отложен номер интервала, без указания абсолютных величин, а по оси Y — число попаданий в интервал. В таком виде по гистограмме можно оценить лишь характер распределения, но не среднее и не дисперсию. Более подробные данные приложены на дискете.

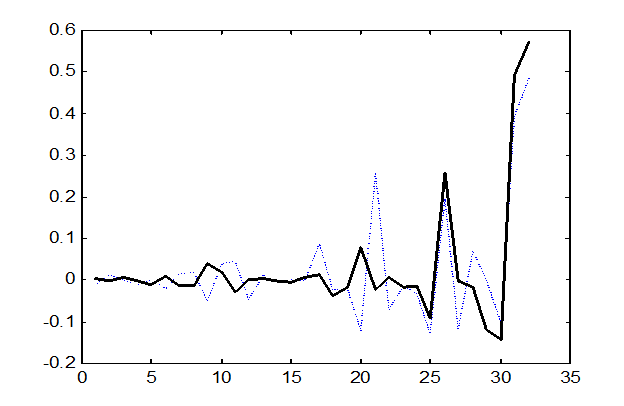
a)

 

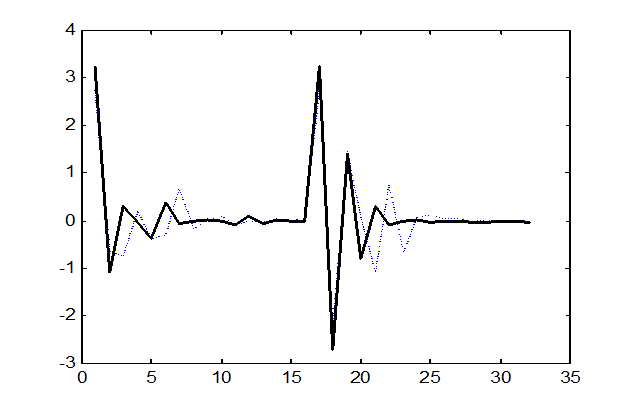
б)

Рис. 9.5. Спектры группы 1 (“- - - -“) и группы 2 (“----“)
в базисах а)Добеши-2 и б)Фурье

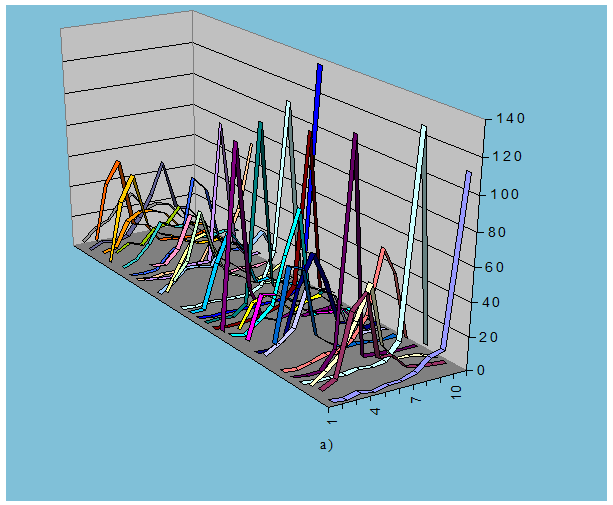
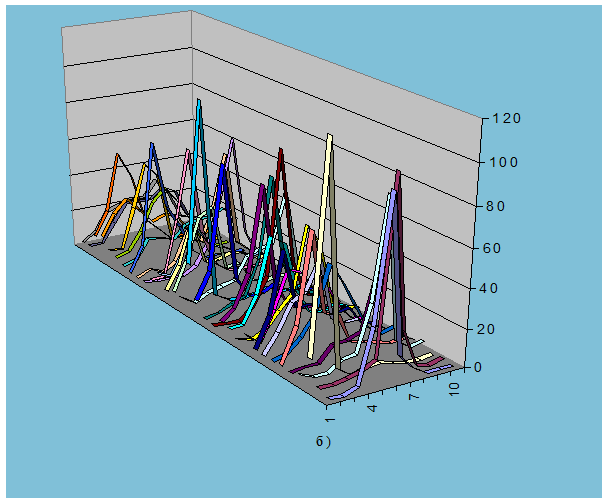
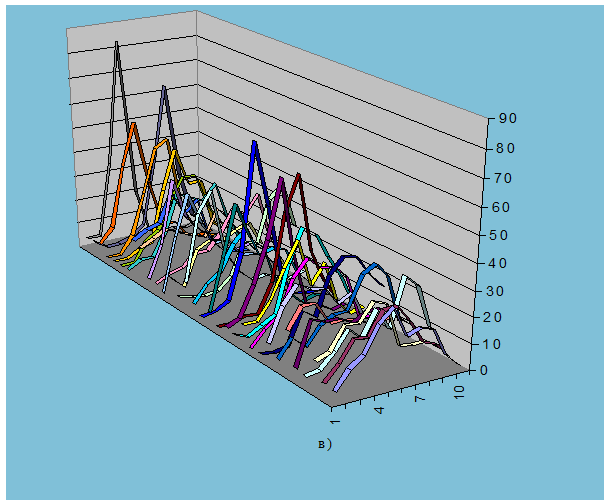
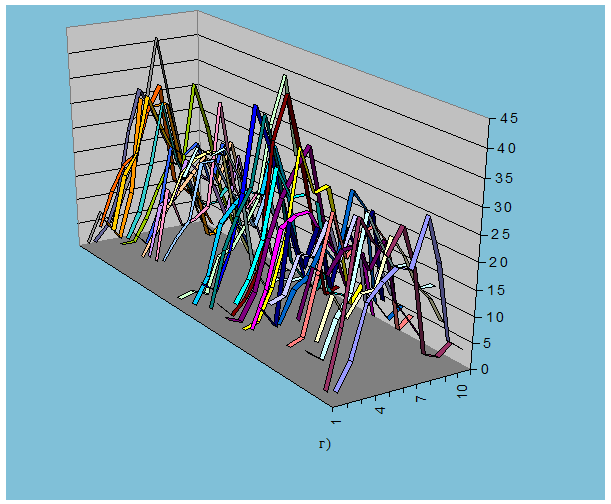
Рис. 9.6. Гистограммы распределения спектральных составляющих для спектров в базисах: а)Добеши-2, группа выборок 1, б)Добеши-2, группа выборок 2,
в)Фурье, группа выборок 1, г)Фурье, группа выборок 2

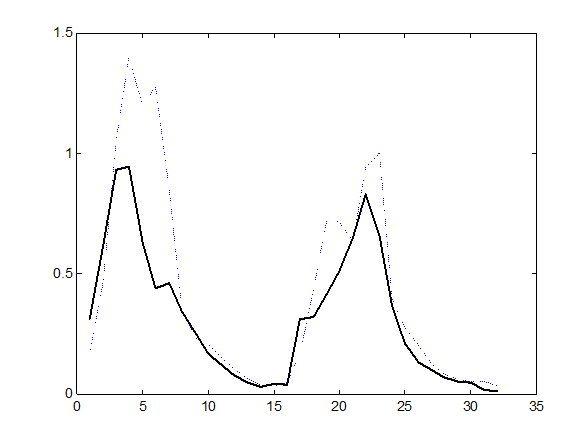
·  Оценки дисперсий спектральных составляющих

.

(9.3)

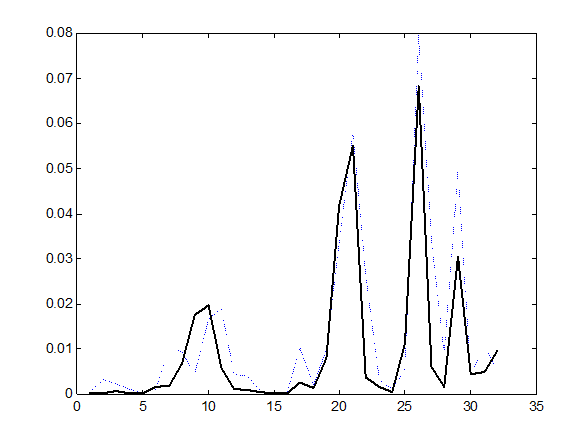
а)

б)

Рис. 9.7. Оценки дисперсий спектральных составляющих выборок
групп 1 (“ - - - - “) и 2 (“----“) в базисах а)Добеши-2 и б)Фурье

·  Оценки третьего и четвертого центральных моментов и коэффициентов асимметрии и эксцесса:

(9.4)

,    .

(9.5)

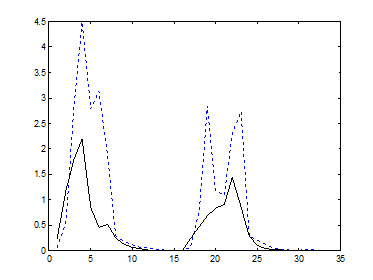
Показаны, соответственно, на рис. 9.8 а,б, 9.9 а,б, 9.10 а,б и 9.11 а,б.

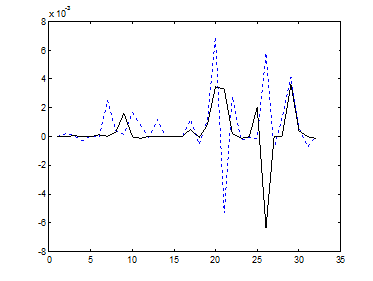
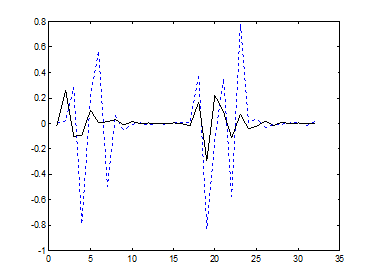
а)                                                                                 б)

Рис. 9.8. Значения третьего центрального момента в базисах а)Добеши-2 и б)Фурье

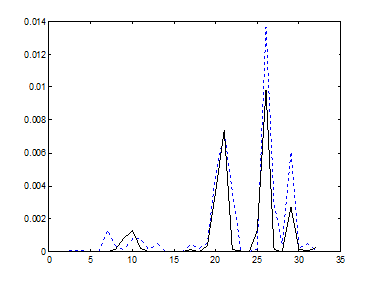
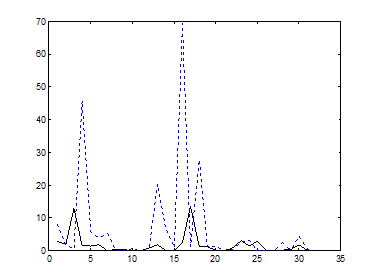
а)                                                                                 б)

Рис. 9.9. Значения четвертого центрального момента в базисах а)Добеши-2 и б)Фурье

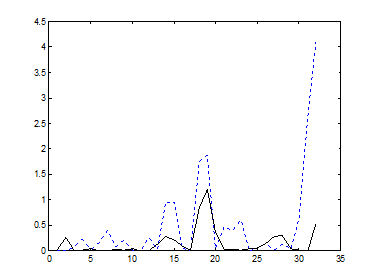
а)                                                                                 б)

Рис. 9.10. Значения коэффициента асимметрии в базисах а)Добеши-2 и б)Фурье

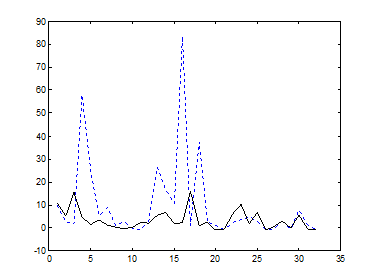
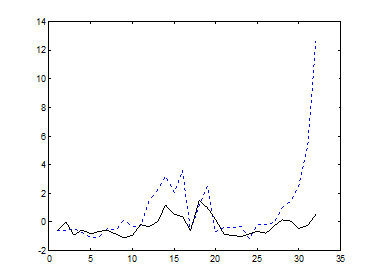
а)                                                                                 б)

Рис. 9.11. Значения коэффициента эксцесса в базисах а)Добеши-2 и б)Фурье

·  Для оценки взаимозависимости спектральных составляющих были вычислены матрицы корреляции

(9.6)

Для быстрой оценки степени коррелированности для каждой корреляционной матрицы была вычислена сумма квадратов элементов

.

(9.7)

Значения S, отнесенные для облегчения сравнения к размеру матрицы (1024 либо 4096 элементов), показаны в таблице 9.1.

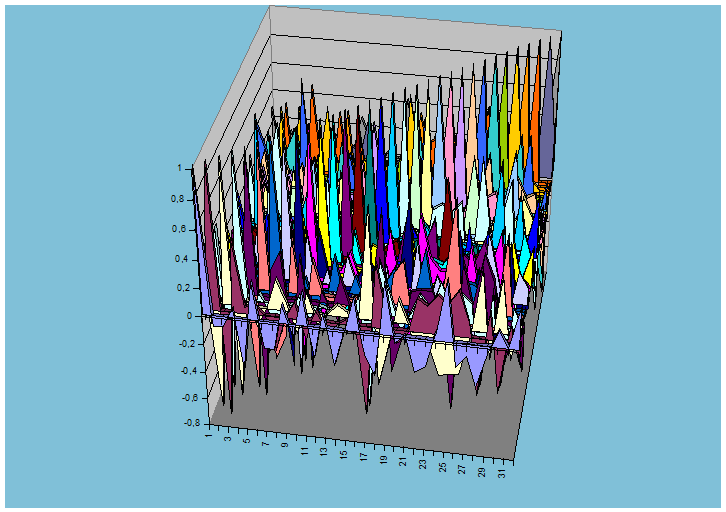
Рис. 9.12. Матрица корреляции для базиса Добеши-2

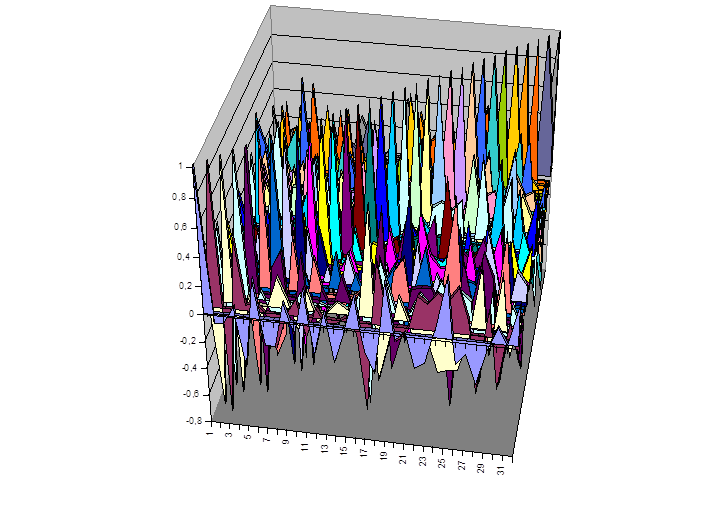
Рис. 9.13. Матрица корреляции для базиса Фурье

Таблица 9.1. Средний квадрат коэффициентов корреляции спектральных составляющих в различных базисах

Тип фильтра	Выборки гр. 1 длина 32	Выборки гр. 2 длина 32	Выборки гр. 1 длина 64	Выборки гр. 2 длина 64
Добеши-1	0,05837	0,06104	0,01092	0,01581
Добеши-2	0,06772	0,06168	0,02428	0,02983
Добеши-3	0,05922	0,07292	0,03156	0,03935
Добеши-4	0,05736	0,05162	0,04016	0,03956
Добеши-5	0,06176	0,05257	0,04616	0,04656
Добеши-6	0,06505	0,05470	0,05447	0,05193
Добеши-7	0,06603	0,06520	0,05937	0,05879
Добеши-8	0,07038	0,06423	0,06886	0,06058
Добеши-9	0,06584	0,07572	0,06260	0,06204
Добеши-10	0,06670	0,07814	0,06626	0,06580
Добеши-11	0,06187	0,06128	0,06660	0,06203
Добеши-12	0,06497	0,06979	0,06921	0,06636
Добеши-13	0,06493	0,06670	0,06917	0,06289
Добеши-14	0,06781	0,06960	0,07521	0,07334
Добеши-15	0,06720	0,08047	0,07658	0,07343
Койфлет-1	0,06322	0,05485	0,03162	0,03457
Койфлет-2	0,05976	0,04961	0,05078	0,05506
Койфлет-3	0,06297	0,05575	0,05826	0,06390
Койфлет-4	0,06467	0,05089	0,06402	0,06522
Койфлет-5	0,06312	0,06075	0,06728	0,07599
Симлет-2	0,06772	0,06168	0,02428	0,02983
Симлет-3	0,05922	0,07292	0,03156	0,03935
Симлет-4	0,06841	0,05837	0,03876	0,04377
Симлет-5	0,06353	0,06169	0,04082	0,04698
Симлет-6	0,06540	0,05676	0,05229	0,05377
Симлет-7	0,05992	0,06522	0,05575	0,05671
Симлет-8	0,06467	0,05539	0,05692	0,06553
Биортогональный-1.3	0,06968	0,05753	0,02188	0,02172
Биортогональный-1.5	0,06286	0,06371	0,02464	0,02680
Биортогональный-2.2	0,05532	0,04836	0,01974	0,02521
Биортогональный-2.4	0,05130	0,05112	0,02033	0,03070
Биортогональный-2.6	0,04863	0,04661	0,02268	0,02894
Биортогональный-2.8	0,05827	0,04836	0,03044	0,03673
Биортогональный-3.1	0,05507	0,04135	0,02259	0,02050
Биортогональный-3.3	0,05152	0,03804	0,02638	0,02412
Биортогональный-3.5	0,04391	0,04354	0,02669	0,02753
Биортогональный-3.7	0,04918	0,04357	0,02887	0,03145
Биортогональный-3.9	0,04809	0,04343	0,03123	0,03158
Биортогональный-4.4	0,05625	0,05231	0,03385	0,04313
Биортогональный-5.5	0,05676	0,05875	0,04997	0,04754
Биортогональный-6.8	0,06413	0,04973	0,04854	0,05536
Фурье	0,06361	0,10078	0,07681	0,11496